题目内容

已知点A（2，0），B（0，2），C（cosα，sinα）．
（Ⅰ）若α∈[-π，0]，且|
AC
|=|
BC
|，求角α；
（Ⅱ）若α∈[
π
2
，π]，且
AC
⊥
BC
，求
sin2α
2
sin(α-
π
4
)-cos2α
的值．
考点：三角函数中的恒等变换应用,平面向量数量积的运算
专题：三角函数的求值,平面向量及应用
分析：（Ⅰ）由|
AC
|=|
BC
|，可得（cosα-2）2+sin2α=cos2α+（sinα-2）2，化简可得sinα=cosα，结合α∈[-π，0]，可得α的值．
（Ⅱ）由
AB
•
BC
=0，整理求得cosα+sinα、2sinαcosα、sinα-cosα的值，从而求得
sin2α
2
sin(α-
π
4
)-cos2α
=
2sinαcosα
(sinα-cosα)[1+(cosα+sinα)]
的值．
解答： 解：（Ⅰ）由题意可得
AC
=（cosα-2，sinα），
BC
=（cosα，sinα-2），
再由|
AC
|=|
BC
|，可得（cosα-2）2+sin2α=cos2α+（sinα-2）2，化简可得sinα=cosα，
又α∈[-π，0]，故α=-
3π
4
．
（Ⅱ）由
AB
•
BC
=0，整理得cosα+sinα=
1
2
，2sinαcosα=-
3
4
，
由于（cosα-sinα）2=（cosα+sinα）2-4sinαcosα=
7
4
，α∈[
π
2
，π]，可得sinα-cosα=
7
2
．
故
sin2α
2
sin(α-
π
4
)-cos2α
=
2sinαcosα
(sinα-cosα)[1+(cosα+sinα)]
=
-
3
4
7
2
×(1+
1
2
)
=-
7
7
．
点评：本题主要考查三角函数的恒等变换及化简求值，两个向量的数量积公式、两个向量垂直的性质，属于基础题．
练习册系列答案
相关题目
某商品降价10%，经过一段时间后恢复原价，需提价
 
．
在△ABC中，B（-
5
，0）、C（
5
，0），AB、AC边上的中线长之和为9．
（Ⅰ）求△ABC重心G的轨迹方程
（Ⅱ）设P为（1）中所求轨迹上任意一点，求cos∠BPC的最小值．
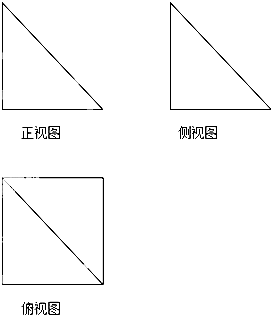一个几何体的三视图如图所示，其中正视图和侧视图是腰长为1的两个全等的等腰直角三角形，若该几何体的所有顶点在同一球面上，则球的表面积是（　　）
A、3π
B、2π
C、π
D、
3π
2
已知函数f（x）=
2
x
，x≥2
(x-1)3，x＜2
若关于x的方程f（x）=k有两个不同的实根，则数k的取值范围是
 
．
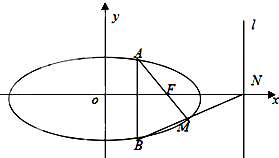如图，已知直线x+ky-1=0所经过的定点F恰好是椭圆C的一个焦点，且椭圆C上的点到点F的最大距离为3．
（Ⅰ）求椭圆C的标准方程；
（Ⅱ）若AB为垂直于x轴的动弦，直线l：x=4与x轴交于点N，直线AF与BN交于点M．
i．求证：点M恒在椭圆C上；
ii．求△AMN面积的最大值．
若直线l的法向量
n
=(1 ， 2)，且经过点M（0，1），则直线l的方程为
 
．
如图所示，某地一天从6～14时的温度变化曲线近似满足y=Asin（ωx+φ）+b（A＞0，ω＞0，|φ|＜π，b∈R），写出这段曲线的函数解析式
 
．
已知数列{an}满足a1=3，an+1=
an-1
an+1
（n∈N*），Tn为数列{an}的前n项之积，则T2010=（　　）
A、
3
2
B、-
1
6
C、
2
3
D、-6

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网