题目内容
已知函数f(x)=|x-a|-
+a,x∈[1,6],a∈R.
(1)若a=1,试判断并用定义证明函数f(x)的单调性;
(2)当a∈(1,6)时,求函数f(x)的最大值的表达式M(a).
| 9 |
| x |
(1)若a=1,试判断并用定义证明函数f(x)的单调性;
(2)当a∈(1,6)时,求函数f(x)的最大值的表达式M(a).
考点:利用导数研究函数的单调性,利用导数求闭区间上函数的最值
专题:导数的综合应用
分析:(1)当a=1时,由x∈[1,6],化简f(x),用单调性定义讨论f(x)的增减性;
(2)由a∈(1,6)知,f(x)=
,分1<a≤3与3<a<6讨论函数的单调性,从而求得f(x)的最大值M(a).
(2)由a∈(1,6)知,f(x)=
|
解答:
解:(1)当a=1,x∈[1,6]时,f(x)为增函数,
证明:∵f(x)=x-
,任取x1,x2∈[1,6],且x1<x2,
则f(x1)-f(x2)=(x1-
)-(x2-
)=
<0,
∴f(x)在[1,6]是增函数;
(2)∵a∈(1,6),∴f(x)=
,
①当1<a<3时,f(x)在[1,a]上是增函数,在[a,6]上也是增函数,
∴当x=6时,f(x)取得最大值
,
②当3<a<6时,f(x)在[1,3]上是增函数,在[3,a]上是减函数,在[a,6]上是增函数,
而f(3)=2a-6,f(6)=
,
当3<a≤
时,2a-6≤
,当x=6时,f(x)取得最大值为
.
当
≤a<6时,2a-6>
,当x=3时,f(x)取得最大值为2a-6.
综上得,M(a)=
证明:∵f(x)=x-
| 9 |
| x |
则f(x1)-f(x2)=(x1-
| 9 |
| x1 |
| 9 |
| x2 |
| (x1-x2)(x1x2+9) |
| x1x2 |
∴f(x)在[1,6]是增函数;
(2)∵a∈(1,6),∴f(x)=
|
①当1<a<3时,f(x)在[1,a]上是增函数,在[a,6]上也是增函数,
∴当x=6时,f(x)取得最大值
| 9 |
| 2 |
②当3<a<6时,f(x)在[1,3]上是增函数,在[3,a]上是减函数,在[a,6]上是增函数,
而f(3)=2a-6,f(6)=
| 9 |
| 2 |
当3<a≤
| 21 |
| 4 |
| 9 |
| 2 |
| 9 |
| 2 |
当
| 21 |
| 4 |
| 9 |
| 2 |
综上得,M(a)=
|
点评:本题考查了含绝对值的函数的单调性的判断与证明以及函数的最值的求法问题,也考查了分类讨论思想与化归思想.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
在各项均为正的数列{an}中,已知2an=3an+1,a2•a5=
,则通项an为( )
| 8 |
| 27 |
A、(
| ||
B、(
| ||
C、(
| ||
D、(
|
一个几何体的三视图如图所示,则该几何体的体积为( )


| A、55 | ||
| B、54 | ||
C、75+4
| ||
D、55+2
|
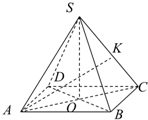 如图,设S-ABCD是一个高为3的四棱锥,底面ABCD是边长为2的正方形,顶点S在底面上的射影是正方形ABCD的中心.K是棱SC的中点.试求直线AK与平面SBC所成角的大小.
如图,设S-ABCD是一个高为3的四棱锥,底面ABCD是边长为2的正方形,顶点S在底面上的射影是正方形ABCD的中心.K是棱SC的中点.试求直线AK与平面SBC所成角的大小.