题目内容
已知定义在实数集R上的偶函数f（x），当x≥0时，f（x）=-x+2；则不等式f（x）-x2≥0的解集为 ．
考点：函数奇偶性的判断
专题：函数的性质及应用
分析：利用f（-x）=f（x），求出当x＜0时，f（x）的解析式，然后解不等式．
解答：
解：当x≥0时，f（x）=-x+2；则不等式f（x）-x2≥0
∴-x+2-x2≥0，
解得，0≤x≤1，
令x＜0，则-x＞0，
∴f（-x）=-（-x）+2，
∵f（-x）=f（x），
∴f（x）=x+2，x＜0，
当x＜0时，f（x）-x2≥0
∴x+2-x2≥0，
解得，-1≤x＜0，
∴不等式f（x）-x2≥0的解集为：1≤x≤1．
故答案为：[-1，1]
∴-x+2-x2≥0，
解得，0≤x≤1，
令x＜0，则-x＞0，
∴f（-x）=-（-x）+2，
∵f（-x）=f（x），
∴f（x）=x+2，x＜0，
当x＜0时，f（x）-x2≥0
∴x+2-x2≥0，
解得，-1≤x＜0，
∴不等式f（x）-x2≥0的解集为：1≤x≤1．
故答案为：[-1，1]
点评：本题考查偶函数象的性质，用此结论转化不等式，这是解本题的最合适的办法．
练习册系列答案
相关题目
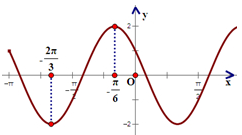如图所示为函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜π）的部分图象．
函数y=Asin（ωx+ϕ）（A＞0，ω＞0，|ϕ|＜π）的图象如图所示，则该函数的解析式为y=