题目内容
11.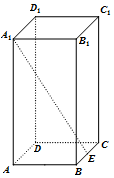 如图,长方体ABCD-A1B1C1D1中,$AB=BC=\frac{1}{2}A{A_1}$,E为BC的中点,则异面直线A1E与D1C1所成角的正切值为( )
如图,长方体ABCD-A1B1C1D1中,$AB=BC=\frac{1}{2}A{A_1}$,E为BC的中点,则异面直线A1E与D1C1所成角的正切值为( )| A. | 2 | B. | $\frac{{4\sqrt{5}}}{5}$ | C. | $\frac{{\sqrt{17}}}{2}$ | D. | $\frac{{2\sqrt{21}}}{21}$ |
分析 以D原点,DA为x轴,AC为y轴,DD1为z轴,建立空间直角系,利用向量法能求出异面直线A1E与D1C1所成角的正切值.
解答 解:以D原点,DA为x轴,AC为y轴,DD1为z轴,建立空间直角系,
设$AB=BC=\frac{1}{2}A{A_1}$=1,则A1(1,0,2),E($\frac{1}{2}$,1,0),C1(0,1,2),D1(0,0,2),
$\overrightarrow{{A}_{1}E}$=(-$\frac{1}{2}$,1,-2),$\overrightarrow{{D}_{1}{C}_{1}}$=(0,1,0),
设异面直线A1E与D1C1所成角为θ,
则cosθ=$\frac{|\overrightarrow{{A}_{1}E}•\overrightarrow{{D}_{1}{C}_{1}}|}{|\overrightarrow{{A}_{1}E}|•|\overrightarrow{{D}_{1}{C}_{1}}|}$=$\frac{1}{\sqrt{\frac{21}{4}}•\sqrt{1}}$=$\frac{2}{\sqrt{21}}$,
sinθ=$\sqrt{1-(\frac{2}{\sqrt{21}})^{2}}$=$\frac{\sqrt{17}}{\sqrt{21}}$,
∴tanθ=$\frac{\frac{\sqrt{17}}{\sqrt{21}}}{\frac{2}{\sqrt{21}}}$=$\frac{\sqrt{17}}{2}$.
∴异面直线A1E与D1C1所成角的正切值为$\frac{\sqrt{17}}{2}$.
故选:C.
点评 本题考查异面直线所成角的正切值的求法,是中档题,解题时要认真审题,注意向量法的合理运用.

| A. | 8 | B. | 4 | C. | 6 | D. | 2 |
| A. | ?x0∈R,使得x2-2x-3>0成立 | B. | ?x0∈R,使得x2-2x-3≥0成立 | ||
| C. | ?x∈R,x2-2x-3<0恒成立 | D. | ?x∈R,x2-2x-3≥0恒成立 |
| A. | |a|<|b| | B. | $\frac{1}{a}>\frac{1}{b}$ | C. | sina>sinb | D. | lna>lnb |
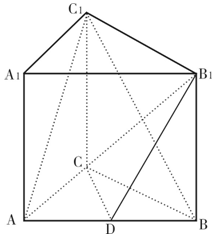 如图,在三棱柱ABC-A1B1C1中,CC1⊥底面ABC,AC=3,BC=4,AB=5,点D是AB的中点.
如图,在三棱柱ABC-A1B1C1中,CC1⊥底面ABC,AC=3,BC=4,AB=5,点D是AB的中点.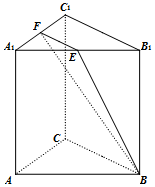 三棱柱ABC-A1B1C1中,AB=AC,侧棱AA1⊥平面ABC,E,F分别为A1B1,A1C1的中点.
三棱柱ABC-A1B1C1中,AB=AC,侧棱AA1⊥平面ABC,E,F分别为A1B1,A1C1的中点.