题目内容
6．实数x，y满足不等式组$\left\{\begin{array}{l}{y≤3}\\{3x+7y-24≤0}\\{x+4y-8≥0}\end{array}\right.$，则z=|x|+|y|的最小值是（ ）| A． | 8 | B． | 4 | C． | 6 | D． | 2 |
分析 作出不等式组对应的平面区域，得到y≥0，然后根据目标函数的几何意义利用图象平移进行求解即可．
解答 
解：作出不等式组对应的平面区域如图：
由图象知y≥0，
则z=|x|+|y|=|x|+y，
即y=-|x|+z．
平移曲线y=-|x|+z，
由图象知当y=-|x|+z经过点A（0，2）时，
曲线y=-|x|+z的截距最小，
此时最小值z=2，
故选：D
点评 本题主要考查线性规划的应用，根据条件判断y≥0是解决本题的关键．
练习册系列答案
相关题目
16．以下四个命题中，错误命题的序号是（ ）
| A． | △ABC中，若a＞b，则sinA＞sinB | |
| B． | 函数y=f（x）在x=x0处取得极值的充要条件是f'（x0）=0 | |
| C． | 等差数列{an}中，a4=4，a5+a11=16则a12=12 | |
| D． | 双曲线$\frac{x^2}{16}-\frac{y^2}{9}=1$的焦点到渐近线的距离3． |
17．集合M={-1，0，1}，N={x∈Z|-1＜x＜1}，则M∩N等于（ ）
| A． | {-1，0，1} | B． | {-1} | C． | {1} | D． | {0} |
14．已知正数a，b，c满足2a-b+c=0，则$\frac{ac}{{b}^{2}}$的最大值为（ ）
| A． | 8 | B． | 2 | C． | $\frac{1}{8}$ | D． | $\frac{1}{6}$ |
1．
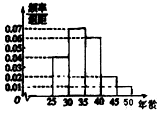2015年10月十八届五中全会决定2016年1月1日起全国统一实施全面两孩政策，为了了解适龄民众对放开生育二胎政策的态度，某市进行了一次民意调查，参与调查的100位市民中，年龄分布情况如图所示，并得到适龄民众对放开生育二胎政策的态度数据如表：
（1）填写上面的2×2列联表；
（2）根据调查数据，有多少的把握认为“生二胎与年龄有关”，说明理由；
（3）调查对象中决定生二胎的民众有六人分别来自三个不同的家庭且为父子，各自家庭都有一个约定：父亲先生二胎，然后儿子生二胎，则这个三个家庭“二胎出生的日期的先后顺序”有多少种？
参考数据：
（参考公式：K2=$\frac{n（ad-bc）^{2}}{（a+b）（c+d）（a+c）（b+d）}$，其中n=a+b+c+d）
2015年10月十八届五中全会决定2016年1月1日起全国统一实施全面两孩政策，为了了解适龄民众对放开生育二胎政策的态度，某市进行了一次民意调查，参与调查的100位市民中，年龄分布情况如图所示，并得到适龄民众对放开生育二胎政策的态度数据如表：| 生二胎 | 不生二胎 | 合计 | |
| 25～35岁 | 45 | 10 | 55 |
| 35～50岁 | 30 | 15 | 45 |
| 合计 | 75 | 25 | 100 |
（2）根据调查数据，有多少的把握认为“生二胎与年龄有关”，说明理由；
（3）调查对象中决定生二胎的民众有六人分别来自三个不同的家庭且为父子，各自家庭都有一个约定：父亲先生二胎，然后儿子生二胎，则这个三个家庭“二胎出生的日期的先后顺序”有多少种？
参考数据：
| P（K2＞k） | 0.15 | 0.10 | 0.05 | 0.010 |
| k | 2.072 | 2.076 | 3.841 | 6.635 |
11．
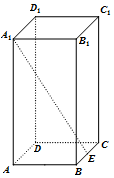如图，长方体ABCD-A1B1C1D1中，$AB=BC=\frac{1}{2}A{A_1}$，E为BC的中点，则异面直线A1E与D1C1所成角的正切值为（ ）
如图，长方体ABCD-A1B1C1D1中，$AB=BC=\frac{1}{2}A{A_1}$，E为BC的中点，则异面直线A1E与D1C1所成角的正切值为（ ）| A． | 2 | B． | $\frac{{4\sqrt{5}}}{5}$ | C． | $\frac{{\sqrt{17}}}{2}$ | D． | $\frac{{2\sqrt{21}}}{21}$ |
