题目内容
2．已知函数f（x）满足f（ab）=f（a）+f（b），且f（2）=p，f（3）=q，那么f（18）=p+2q．分析 由已知中f（ab）=f（a）+f（b），可得f（18）=f（2）+f（3）+f（3），进而得到答案．
解答 解：∵函数f（x）满足f（ab）=f（a）+f（b），
∴f（18）=f（2）+f（3）+f（3），
又∵f（2）=p，f（3）=q，
∴f（18）=p+2q，
故答案为：p+2q
点评 本题考查的知识点是抽象函数的应用，函数求值，转化思想，难度中档．
练习册系列答案
相关题目
12．双曲线$\frac{x^2}{16}-\frac{y^2}{8}=1$的实轴长是（ ）
| A． | 2 | B． | $4\sqrt{2}$ | C． | $2\sqrt{2}$ | D． | 8 |
13．春节是旅游消费旺季，某大型商场通过对春节前后20天的调查，得到部分日经济收入Q与这20天中的第x天（x∈N+）的部分数据如表：
（1）根据表中数据，结合函数图象的性质，从下列函数模型中选取一个最恰当的函数模型描述Q与x的变化关系，只需说明理由，不用证明．
①Q=ax+b，②Q=-x2+ax+b，③Q=ax+b，④Q=b+logax．
（2）结合表中的数据，根据你选择的函数模型，求出该函数的解析式，并确定日经济收入最高的是第几天；并求出这个最高值．
| 天数x（天） | 3 | 5 | 7 | 9 | 11 | 13 | 15 |
| 日经济收入Q（万元） | 154 | 180 | 198 | 208 | 210 | 204 | 190 |
①Q=ax+b，②Q=-x2+ax+b，③Q=ax+b，④Q=b+logax．
（2）结合表中的数据，根据你选择的函数模型，求出该函数的解析式，并确定日经济收入最高的是第几天；并求出这个最高值．
10．若幂函数y=xm是偶函数，且x∈（0，+∞）时为减函数，则实数m的值可能为（ ）
| A． | -2 | B． | $-\frac{1}{2}$ | C． | $\frac{1}{2}$ | D． | 2 |
17．集合M={-1，0，1}，N={x∈Z|-1＜x＜1}，则M∩N等于（ ）
| A． | {-1，0，1} | B． | {-1} | C． | {1} | D． | {0} |
14．已知正数a，b，c满足2a-b+c=0，则$\frac{ac}{{b}^{2}}$的最大值为（ ）
| A． | 8 | B． | 2 | C． | $\frac{1}{8}$ | D． | $\frac{1}{6}$ |
11．
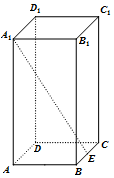如图，长方体ABCD-A1B1C1D1中，$AB=BC=\frac{1}{2}A{A_1}$，E为BC的中点，则异面直线A1E与D1C1所成角的正切值为（ ）
如图，长方体ABCD-A1B1C1D1中，$AB=BC=\frac{1}{2}A{A_1}$，E为BC的中点，则异面直线A1E与D1C1所成角的正切值为（ ）| A． | 2 | B． | $\frac{{4\sqrt{5}}}{5}$ | C． | $\frac{{\sqrt{17}}}{2}$ | D． | $\frac{{2\sqrt{21}}}{21}$ |
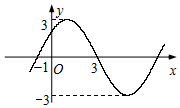函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，φ∈[0，2π））的图象，如图所示，则f（2016）的值为$\frac{{3\sqrt{2}}}{2}$．