题目内容
16.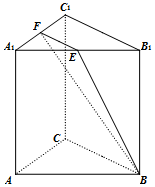 三棱柱ABC-A1B1C1中,AB=AC,侧棱AA1⊥平面ABC,E,F分别为A1B1,A1C1的中点.
三棱柱ABC-A1B1C1中,AB=AC,侧棱AA1⊥平面ABC,E,F分别为A1B1,A1C1的中点.(Ⅰ)求证:B1C1∥面BEF;
(Ⅱ)过点A存在一条直线与平面BEF垂直,请你在图中画出这条直线(保留作图痕迹,不必说明理由).
分析 (Ⅰ)利用已知及三角形的中位线定理可证EF∥B1C1,进而利用线面平行的判定定理即可得证.
(Ⅱ)利用线面垂直的性质及判定定理即可作图得解.
解答 (本题满分8分)
证明:(Ⅰ)∵E,F分别为A1B1,A1C1的中点,
∴EF∥B1C1.
又∵EF?面BEF,B1C1?面BEF,
∴B1C1∥面BEF. …(5分)
(Ⅱ)作图如下:
…(8分)
点评 本题主要考查了三角形的中位线定理,线面平行的判定定理,线面垂直的性质及判定定理的综合应用,考查了数形结合思想,考查了空间想象能力和推理论证能力,属于中档题.

练习册系列答案
相关题目
6.过点P(3,2)且在两坐标轴上的截距相等的直线方程是( )
| A. | x-y-1=0 | B. | x+y-5=0或2x-3y=0 | ||
| C. | x+y-5=0 | D. | x-y-1=0或2x-3y=0 |
11.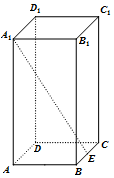 如图,长方体ABCD-A1B1C1D1中,$AB=BC=\frac{1}{2}A{A_1}$,E为BC的中点,则异面直线A1E与D1C1所成角的正切值为( )
如图,长方体ABCD-A1B1C1D1中,$AB=BC=\frac{1}{2}A{A_1}$,E为BC的中点,则异面直线A1E与D1C1所成角的正切值为( )
 如图,长方体ABCD-A1B1C1D1中,$AB=BC=\frac{1}{2}A{A_1}$,E为BC的中点,则异面直线A1E与D1C1所成角的正切值为( )
如图,长方体ABCD-A1B1C1D1中,$AB=BC=\frac{1}{2}A{A_1}$,E为BC的中点,则异面直线A1E与D1C1所成角的正切值为( )| A. | 2 | B. | $\frac{{4\sqrt{5}}}{5}$ | C. | $\frac{{\sqrt{17}}}{2}$ | D. | $\frac{{2\sqrt{21}}}{21}$ |
1.直线x-y+1=0的倾斜角为( )
| A. | -45° | B. | -30° | C. | 45° | D. | 135° |
8.已知集合A={x|$\frac{x+1}{x-2}$<0},集合B=N,则A∩B=( )
| A. | {-1,0,1} | B. | {1} | C. | {0,1} | D. | {-1,0} |
5.中国历法推测遵循以测为辅、以算为主的原则.例如《周髀算经》和《易经》里对二十四节气的晷(guǐ)影长的记录中,冬至和夏至的晷影长是实测得到的,其它节气的晷影长则是按照等差数列的规律计算得出的.下表为《周髀算经》对二十四节气晷影长的记录,其中115.1$\frac{4}{6}$寸表示115寸1$\frac{4}{6}$分(1寸=10分).
已知《易经》中记录的冬至晷影长为130.0寸,夏至晷影长为14.8寸,那么《易经》中所记录的惊蛰的晷影长应为( )
| 节气 | 冬至 | 小寒 (大雪) | 大寒 (小雪) | 立春 (立冬) | 雨水 (霜降) | 惊蛰 (寒露) | 春分 (秋分) | 清明 (白露) | 谷雨 (处暑) | 立夏 (立秋) | 小满 (大暑) | 芒种 (小暑) | 夏至 |
| 晷影长 (寸) | 135 | 125$\frac{5}{6}$ | 115.1$\frac{4}{6}$ | 105.2$\frac{4}{6}$ | 95.3$\frac{2}{6}$ | $85.4\frac{2}{6}$ | 75.5 | 66.5$\frac{5}{6}$ | $55.6\frac{4}{6}$ | 45.7$\frac{3}{6}$ | 35.8$\frac{2}{6}$ | 25.9$\frac{1}{6}$ | 16.0 |
| A. | 72.4寸 | B. | 81.4寸 | C. | 82.0寸 | D. | 91.6寸 |
6.若a,b,c∈R,则下列说法正确的是( )
| A. | 若a>b,则a-c>b-c | B. | 若a>b,则$\frac{1}{a}<\frac{1}{b}$ | C. | 若a>b,则a2>b2 | D. | 若a>b,则ac2>bc2 |