题目内容
1.已知函数f(x)=ln(a-$\frac{1}{x}$)(a∈R).若关于x的方程ln[(4-a)x+2a-5]-f(x)=0的解集中恰好有一个元素,则实数a的取值范围为(1,2]∪{3,4}.分析 根据对数的运算法则进行化简,转化为一元二次方程,讨论a的取值范围进行求解即可.
解答 解:由ln[(4-a)x+2a-5]-f(x)=0,
得ln[( 4-a)x+2a-5]=ln(a-$\frac{1}{x}$),
即a-$\frac{1}{x}$=(4-a)x+2a-5>0,①
则(a-4)x2-(a-5)x-1=0,
即(x-1)[(a-4)x+1]=0,②,
当a=4时,方程②的解为x=1,代入①,成立;
当a=3时,方程②的解为x=1,代入①,成立;
当a≠4且a≠3时,方程②的解为x=1或x=-$\frac{1}{a-4}$,
若x=1是方程①的解,则a-$\frac{1}{x}$=a-1>0,即a>1,
若x=-$\frac{1}{a-4}$是方程①的解,则a-$\frac{1}{x}$=2a-4>0,即a>2,
则要使方程①有且仅有一个解,则1<a≤2.
综上,关于x的方程ln[(4-a)x+2a-5]-f(x)=0的解集中恰好有一个元素,
则a的取值范围是1<a≤2,或a=3或a=4,
故答案为:(1,2]∪{3,4}.
点评 本题考查对数的运算性质,考查数学转化思想方法和分类讨论的数学思想方法,属中档题.

练习册系列答案
相关题目
11.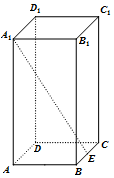 如图,长方体ABCD-A1B1C1D1中,$AB=BC=\frac{1}{2}A{A_1}$,E为BC的中点,则异面直线A1E与D1C1所成角的正切值为( )
如图,长方体ABCD-A1B1C1D1中,$AB=BC=\frac{1}{2}A{A_1}$,E为BC的中点,则异面直线A1E与D1C1所成角的正切值为( )
 如图,长方体ABCD-A1B1C1D1中,$AB=BC=\frac{1}{2}A{A_1}$,E为BC的中点,则异面直线A1E与D1C1所成角的正切值为( )
如图,长方体ABCD-A1B1C1D1中,$AB=BC=\frac{1}{2}A{A_1}$,E为BC的中点,则异面直线A1E与D1C1所成角的正切值为( )| A. | 2 | B. | $\frac{{4\sqrt{5}}}{5}$ | C. | $\frac{{\sqrt{17}}}{2}$ | D. | $\frac{{2\sqrt{21}}}{21}$ |
6.若a,b,c∈R,则下列说法正确的是( )
| A. | 若a>b,则a-c>b-c | B. | 若a>b,则$\frac{1}{a}<\frac{1}{b}$ | C. | 若a>b,则a2>b2 | D. | 若a>b,则ac2>bc2 |
13.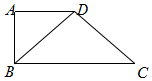 如图所示,四边形ABCD中,AD∥BC,AD=AB,∠BCD=45°,∠BAD=90°,将
如图所示,四边形ABCD中,AD∥BC,AD=AB,∠BCD=45°,∠BAD=90°,将
△ABD沿BD折起,使面ABD⊥面BCD,连结AC,则下列命题正确的是( )
 如图所示,四边形ABCD中,AD∥BC,AD=AB,∠BCD=45°,∠BAD=90°,将
如图所示,四边形ABCD中,AD∥BC,AD=AB,∠BCD=45°,∠BAD=90°,将△ABD沿BD折起,使面ABD⊥面BCD,连结AC,则下列命题正确的是( )
| A. | 面ABD⊥面ABC | B. | 面ADC⊥面BDC | C. | 面ABC⊥面BDC | D. | 面ADC⊥面ABC |
10.已知全集U={1,2,3,4},集合A={1,2},集合B={2,3},则∁U(A∪B)=( )
| A. | {4} | B. | {3} | C. | {1,3,4} | D. | {3,4} |
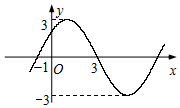 函数f(x)=Asin(ωx+φ)(A>0,ω>0,φ∈[0,2π))的图象,如图所示,则f(2016)的值为$\frac{{3\sqrt{2}}}{2}$.
函数f(x)=Asin(ωx+φ)(A>0,ω>0,φ∈[0,2π))的图象,如图所示,则f(2016)的值为$\frac{{3\sqrt{2}}}{2}$.