题目内容
19．在下列条件下，分别求出有多少种不同的做法？（1）5个不同的球，放入4个不同的盒子，每盒至少一球；
（2）5个相同的球，放入4个不同的盒子，每盒至少一球．
分析 （1）根据分步计数原理，第一步从5个球种选出2个组成复合元素，再把4个元素（包含一个复合元素）放入4个不同的盒子中，问题得以解决；
（2）5个相同的球，放入4个不同的盒子，每盒至少一球，有C43种方法．
解答 解：（1）第一步从5个球种选出2个组成复合元素共有C52种方法，
再把4个元素（包含一个复合元素）放入4个不同的盒子中有A44种，
根据分步计数原理放球的方法共有C52A44=240种---（5分）
（2）C43=4----（10分）
点评 本题主要考查了排列组合混合问题，先选后排是关键．
练习册系列答案
相关题目
9．在平行六面体ABCD-A1B1C1D1中，化简$\overrightarrow{AB}+\overrightarrow{C{C_1}}-\overrightarrow{DB}$为（ ）
| A． | $\overrightarrow{A{C}_{1}}$ | B． | $\overrightarrow{C{A}_{1}}$ | C． | $\overrightarrow{A{D_1}}$ | D． | $\overrightarrow{{D_1}A}$ |
10．若幂函数y=xm是偶函数，且x∈（0，+∞）时为减函数，则实数m的值可能为（ ）
| A． | -2 | B． | $-\frac{1}{2}$ | C． | $\frac{1}{2}$ | D． | 2 |
14．已知正数a，b，c满足2a-b+c=0，则$\frac{ac}{{b}^{2}}$的最大值为（ ）
| A． | 8 | B． | 2 | C． | $\frac{1}{8}$ | D． | $\frac{1}{6}$ |
11．
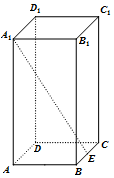如图，长方体ABCD-A1B1C1D1中，$AB=BC=\frac{1}{2}A{A_1}$，E为BC的中点，则异面直线A1E与D1C1所成角的正切值为（ ）
如图，长方体ABCD-A1B1C1D1中，$AB=BC=\frac{1}{2}A{A_1}$，E为BC的中点，则异面直线A1E与D1C1所成角的正切值为（ ）| A． | 2 | B． | $\frac{{4\sqrt{5}}}{5}$ | C． | $\frac{{\sqrt{17}}}{2}$ | D． | $\frac{{2\sqrt{21}}}{21}$ |
8．已知集合A={x|$\frac{x+1}{x-2}$＜0}，集合B=N，则A∩B=（ ）
| A． | {-1，0，1} | B． | {1} | C． | {0，1} | D． | {-1，0} |