题目内容
已知函数y=sin(ωx+φ)(ω>0,-
<φ<
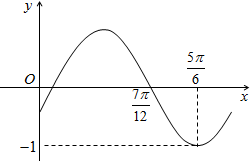
)的部分图象如图所示,则( )
| π |
| 2 |
| π |
| 2 |

A、ω=2,φ=-
| ||
B、ω=2,φ=
| ||
C、ω=1,φ=-
| ||
D、ω=1,φ=
|
考点:由y=Asin(ωx+φ)的部分图象确定其解析式
专题:三角函数的图像与性质
分析:由周期求出ω,由特殊点的坐标求出φ的值,从而得出结论.
解答:
解:由函数的图象可得
•T=
•
=(
-
),∴ω=2.
再把点(
,0)代入函数的解析式可得sin( 2×
+φ)=0,化简可得 sin(
+φ)=0,
结合-
<φ<
,可得 φ=-
,
故选:A.
| 1 |
| 4 |
| 1 |
| 4 |
| 2π |
| ω |
| 5π |
| 6 |
| 7π |
| 12 |
再把点(
| 7π |
| 12 |
| 7π |
| 12 |
| 7π |
| 6 |
结合-
| π |
| 2 |
| π |
| 2 |
| π |
| 6 |
故选:A.
点评:本题主要考查由函数y=Asin(ωx+φ)的部分图象求解析式,由周期求出ω,由特殊点的坐标求出φ的值,属于基础题.

练习册系列答案
 步步高达标卷系列答案
步步高达标卷系列答案
相关题目
已知函数f(x)=
+
的两个极值点x1,x2,且x1,x2分别是一个椭圆和一个双曲线的离心率,点P(m,n)表示的平面区域为D,若函数y=ax+4-7(a>1)的图象存在区域D内的点,则实数a的取值范围是( )
| x3 |
| 3 |
| mx2+(m+n)x+1 |
| 2 |
| A、(2,+∞) |
| B、[2,+∞) |
| C、[1,2] |
| D、(1,2) |
在△ABC中,|
|=2,|
|=1,
•
=-1,则△ABC的外接圆半径是( )
| BA |
| AC |
| BA |
| AC |
| A、1 | ||||
| B、2 | ||||
C、
| ||||
D、
|
阅读如图所示的程序框图,运行相应的程序,输出的结果是( )


| A、16 | B、8 | C、4 | D、2 |
设函数f(x)在R上单调递减,且对于任意实数m,n,总有f(m+n)=f(m)•f(n),设A={(x,y)|f(x2)•f(y2)>f(1)},B={(x,y)|f(ax-y+2)=1,a∈R},若A∩B=∅,则a的取值范围是( )
A、-
| ||||
B、-
| ||||
C、0≤a≤
| ||||
D、-
|
若函数f(x),g(x)的定义域和值域都是R,则f(x)>g(x)(x∈R)成立的充要条件是( )
| A、?x0∈R,f(x0)>g(x0) |
| B、有无穷多个x∈R,使得f(x)>g(x) |
| C、?x∈R,f(x)>g(x)+1 |
| D、R中不存在x使得f(x)≤g(x) |
已知c>0,设p:函数f(x)=cx在R上单调递减,q:函数g(x)=
的定义域是R,如果“p且q”是假命题,“p或q”是真命题,那么c的取值范围是( )
| 1 |
| 2cx2+2x+1 |
A、(
| ||
B、(
| ||
C、(0,
| ||
D、(0,
|
定义:eiθ=cosθ+isinθ(i为虚数单位),若ei
+1-
i=eiα,则α角可能是( )
| 2π |
| 3 |
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|
设函数f(x)=
,若f(x)>f(0),则x的取值范围是( )
|
| A、(0,2)∪(3,+∞) |
| B、(3,+∞) |
| C、(0,1)∪(2,+∞) |
| D、(0,2) |