题目内容
已知O是三角形ABC的外心，AB=6，AC=10，若
=x
+y
，且2x+10y=5，则三角形ABC的面积为 ．
| AO |
| AB |
| AC |
考点：向量在几何中的应用
专题：平面向量及应用
分析：取AC中点为D，则OD⊥AC，把
写为
+
，然后用两种方法写出
•
，由数量积相等结合2x+10y=5求得cos∠BAC，进一步得到其正弦值，代入三角形的面积公式求得三角形ABC的面积．
| AO |
| AD |
| DO |
| AO |
| AC |
解答：
解：当B为直角时，由AB=6，AC=10，求得BC=8，满足
=x
+y
，且2x+10y=5，
此时三角形ABC的面积为S=
•AB•AC=
×6×8=24；
当B不是直角时，
取AC中点为D，则OD⊥AC，
⊥
，
∵
=
+
，
∴
•
=
•
+
•
=|
||
|cos0=5×10=50．
又
=x
+y
，
∴
•
=(x
+y
)•
=x
•
+y|
|2=x|
||
|cos∠BAC+y|
|2
=60x•cos∠BAC+100y，
∴60x•cos∠BAC+100y=5，
又2x+10y=5，
cos∠BAC=
，则sin∠BAC=
．
∴三角形ABC的面积为S=
AB•AC•sin∠BAC=
×6×10×
=20
．
故答案为：24或20
．
| AO |
| AB |
| AC |
此时三角形ABC的面积为S=
| 1 |
| 2 |
| 1 |
| 2 |
当B不是直角时，
取AC中点为D，则OD⊥AC，
| DO |
| AC |
∵
| AO |
| AD |
| DO |
∴
| AO |
| AC |
| AD |
| AC |
| DO |
| AC |
| AD |
| AC |
又
| AO |
| AB |
| AC |
∴
| AO |
| AC |
| AB |
| AC |
| AC |
| AB |
| AC |
| AC |
| AB |
| AC |
| AC |
=60x•cos∠BAC+100y，
∴60x•cos∠BAC+100y=5，
又2x+10y=5，
cos∠BAC=
| 1 |
| 3 |
2
| ||
| 3 |
∴三角形ABC的面积为S=
| 1 |
| 2 |
| 1 |
| 2 |
2
| ||
| 3 |
| 2 |
故答案为：24或20
| 2 |
点评：本题考查了向量在几何中的应用，考查了平面向量的数量积运算，考查了三角形面积公式的应用，是中档题．
练习册系列答案
阅读快车系列答案
相关题目
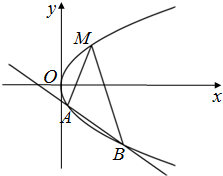如图所示，已知点M（a，3）是抛物线y2=4x上一定点，直线AM、BM的斜率互为相反数，且与抛物线另交于A、B两个不同的点．
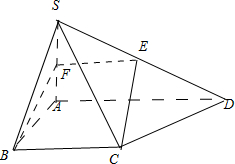在四棱锥S-ABCD中，底面ABCD为直角梯形，其中AD∥BC，∠BAD=90°，SA⊥底面ABCD，SA=AB=BC=2，tan∠SDA=
如图，已知斜三棱柱ABC-A1B1C1，侧面BC1是边长为3的正方形，AA1到侧面BC1的距离为2，E为侧棱CC1上一点，且C1E=1，则三棱锥E-A1B1C1的体积为
如图所示，在矩形ABCD中，AB=3