题目内容
已知椭圆C:
+
=1(a>b>0),左、右两个焦点分别为F1、F2,上顶点M(0,b),△MF1F2为正三角形且周长为6,直线l:x=my+4与椭圆C相交于A、B两点.
(Ⅰ)求椭圆C的方程;
(Ⅱ)求
•
的取值范围.
| x2 |
| a2 |
| y2 |
| b2 |
(Ⅰ)求椭圆C的方程;
(Ⅱ)求
| OA |
| OB |
考点:直线与圆锥曲线的综合问题
专题:综合题,圆锥曲线的定义、性质与方程
分析:(Ⅰ)根据上顶点M(0,b),△MF1F2为正三角形且周长为6,求出几何量,即可求椭圆C的方程;
(Ⅱ)直线l:x=my+4代入椭圆方程,利用韦达定理,结合向量的数量积公式,即可求
•
的取值范围.
(Ⅱ)直线l:x=my+4代入椭圆方程,利用韦达定理,结合向量的数量积公式,即可求
| OA |
| OB |
解答:
解:(Ⅰ)∵上顶点M(0,b),△MF1F2为正三角形且周长为6,
∴a=2,c=1,b=
,
∴椭圆的方程为
+
=1;
(Ⅱ)直线l:x=my+4代入椭圆方程,得(3m2+4)y2+24my+36=0,
由△=(24m)2-4×36×(3m2+4)>0
可得m2>4.
设A(x1,y1),B(x2,y2),
则y1+y2=-
,y1y2=
∴
•
=x1x2+y1y2=(m2+1)y1y2+4m(y1+y2)+16=-4+
,
∵m2>4,
∴3m2+4>16,
∴
•
∈(-4,
).
∴a=2,c=1,b=
| 3 |
∴椭圆的方程为
| x2 |
| 4 |
| y2 |
| 3 |
(Ⅱ)直线l:x=my+4代入椭圆方程,得(3m2+4)y2+24my+36=0,
由△=(24m)2-4×36×(3m2+4)>0
可得m2>4.
设A(x1,y1),B(x2,y2),
则y1+y2=-
| 24m |
| 3m2+4 |
| 36 |
| 3m2+4 |
∴
| OA |
| OB |
| 116 |
| 3m2+4 |
∵m2>4,
∴3m2+4>16,
∴
| OA |
| OB |
| 13 |
| 4 |
点评:本题考查椭圆的方程,考查直线与椭圆的位置关系,考查韦达定理的运用,考查向量的数量积公式,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
若x、y满足约束条件
,则z=x+2y的取值范围是( )
|
| A、[0,4] |
| B、[4,6] |
| C、[2,4] |
| D、[2,6] |
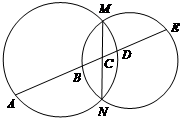 如图,MN为两圆的公共弦,一条直线与两圆及公共弦依次交于A,B,C,D,E,求证:AB•CD=BC•DE.
如图,MN为两圆的公共弦,一条直线与两圆及公共弦依次交于A,B,C,D,E,求证:AB•CD=BC•DE.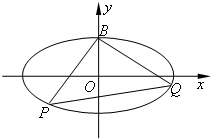 已知椭圆C:
已知椭圆C: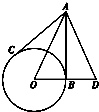 如图,AB、AC为⊙O的切线,B和C是切点,延长OB到D,使BD=OB,连接AD.如果∠DAC=78°,那么∠ADO等于
如图,AB、AC为⊙O的切线,B和C是切点,延长OB到D,使BD=OB,连接AD.如果∠DAC=78°,那么∠ADO等于