题目内容
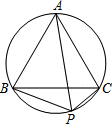如图，P是等边△ABC外接圆 |
| BC |
考点：与圆有关的比例线段
专题：直线与圆
分析：设PA∩BC=D，由△ABC为等边三角形，推导出△ACD∽△APC，从而得到PA•AD=AC2，推导出△BAP∽△DCP，从而得到PA•PD=PB•PC，由此能够证明PA2=AC2+PB•PC．
解答：
证明：设PA∩BC=D，
∵△ABC为等边三角形，∴AB=AC，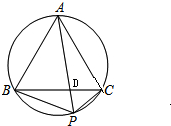
∴∠ACB=∠APC，又∵∠CAD=∠PAC，
∴△ACD∽△APC，
∴
=
，
∴PA•AD=AC2，
∵∠APB=∠APC，∠BAP=∠BCP，
∴△BAP∽△DCP，
∴
=
，
∴PA•PD=PB•PC
∴PA•AD+PA•PD=AC2+PB•PC
∵PA=AD+PD
∴PA2=AC2+PB•PC．
∵△ABC为等边三角形，∴AB=AC，
∴∠ACB=∠APC，又∵∠CAD=∠PAC，
∴△ACD∽△APC，
∴
| PA |
| AC |
| AC |
| AD |
∴PA•AD=AC2，
∵∠APB=∠APC，∠BAP=∠BCP，
∴△BAP∽△DCP，
∴
| PA |
| PC |
| PB |
| PD |
∴PA•PD=PB•PC
∴PA•AD+PA•PD=AC2+PB•PC
∵PA=AD+PD
∴PA2=AC2+PB•PC．
点评：本题考查与圆有关的比例线段的应用，是中档题，解题时要认真审题，注意相似三角形的证明与应用．
练习册系列答案
名校课堂系列答案
相关题目
设全集U={1，2，3，4，5，6}，M={1，2，3}，N={3，4，5}，则（∁UM）∩N=（ ）
| A、{3} |
| B、{4，5} |
| C、{3，4，5} |
| D、（4，5） |
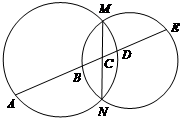如图，MN为两圆的公共弦，一条直线与两圆及公共弦依次交于A，B，C，D，E，求证：AB•CD=BC•DE．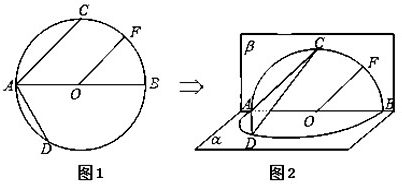
已知椭圆C：