题目内容
已知⊙O的直径为10，弦AB=8，P是弦AB上一个动点，求OP长的取值范围．
考点：与圆有关的比例线段
专题：直线与圆
分析：由几何知识各，当P为AB的中点时，OP最短；当点P与A点或B点重合时，OP最长．由此能求出OP长的取值范围．
解答：
解：由几何知识短，当P为AB的中点时，
OP最短，如图（1）所示，
此时OP=
=3；
当点P与A点或B点重合时，
OP最长，如图（2）所示，
此时OP=OA=5．
∴OP长的取值范围是[3，5]．
OP最短，如图（1）所示，
此时OP=
(
|
当点P与A点或B点重合时，
OP最长，如图（2）所示，
此时OP=OA=5．
∴OP长的取值范围是[3，5]．
点评：本题考查线段长的取值范围的求法，是基础题，解题时要注意数形结合思想的合理运用．
练习册系列答案
相关题目
设全集U={1，2，3，4，5，6}，M={1，2，3}，N={3，4，5}，则（∁UM）∩N=（ ）
| A、{3} |
| B、{4，5} |
| C、{3，4，5} |
| D、（4，5） |
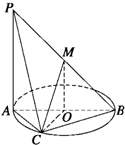如图，AB为圆O的直径，点C在圆周上（异于点A，B），直线PA垂直于圆O所在的平面，点M为线段PB的中点．有以下四个命题：①PA∥平面MOB；②MO∥平面PAC；③OC⊥平面PAC；
④平面PAC⊥平面PBC．其中正确的命题是（ ）
| A、①和② | B、②和③ |
| C、③和④ | D、②和④ |
若x、y满足约束条件
，则z=x+2y的取值范围是（ ）
|
| A、[0，4] |
| B、[4，6] |
| C、[2，4] |
| D、[2，6] |
如图，在平面直角坐标系xOy中，椭圆C：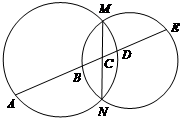
如图，MN为两圆的公共弦，一条直线与两圆及公共弦依次交于A，B，C，D，E，求证：AB•CD=BC•DE．