题目内容
下列命题中，正确命题的序号是 ．
①函数y=sin4x-cos4x的最小正周期是π；
②终边在y轴上的角的集合是{α|α=
，k∈Z}；
③在同一坐标系中，函数y=sinx的图象与函数y=x的图象有3个公共点；
④把函数y=3sin（2x+
）的图象向右平移
得到y=3sin2x的图象．
①函数y=sin4x-cos4x的最小正周期是π；
②终边在y轴上的角的集合是{α|α=
| kπ |
| 2 |
③在同一坐标系中，函数y=sinx的图象与函数y=x的图象有3个公共点；
④把函数y=3sin（2x+
| π |
| 3 |
| π |
| 6 |
考点：命题的真假判断与应用,根的存在性及根的个数判断,三角函数的周期性及其求法,函数y=Asin（ωx+φ）的图象变换
专题：三角函数的图像与性质
分析：①展开平方差公式，利用平方关系结合二倍角余弦公式化简，求出最小正周期后加以判断；
②直接写出终边在y轴上的角的集合加以判断；
③由x∈(0，
)时函数y=sinx与y=x的交点情况，结合函数y=sinx与y=x均为奇函数加以判断；
④直接由函数图象平移得到函数y=3sin（2x+
）的图象向右平移
所得函数解析式，从而判断命题真假．
②直接写出终边在y轴上的角的集合加以判断；
③由x∈(0，
| π |
| 2 |
④直接由函数图象平移得到函数y=3sin（2x+
| π |
| 3 |
| π |
| 6 |
解答：
解：对于①，∵y=sin4x-cos4x=（sin2x-cos2x）（sin2x+cos2x）=-cos2x．
∴函数y=sin4x-cos4x的最小正周期是π，命题①正确；
对于②，终边在y轴上的角的集合是{α|α=kπ+
，k∈Z}，∴命题②错误；
对于③，∵x∈(0，
)时，函数f（x）=x-sinx的导数f′（x）=1-cosx＞0，
∴f（x）＞f（0）=0，
∴x＞sinx，则只有x=0时sin0=0，
又函数y=sinx与y=x均为奇函数，
∴在同一坐标系中，函数y=sinx的图象与函数y=x的图象只有1个公共点，命题③错误；
对于④，把函数y=3sin（2x+
）的图象向右平移
，
得到y=3sin[2(x-
)+
]=3sin2x．
∴命题④正确．
∴正确的命题是①④．
故答案为：①④．
∴函数y=sin4x-cos4x的最小正周期是π，命题①正确；
对于②，终边在y轴上的角的集合是{α|α=kπ+
| π |
| 2 |
对于③，∵x∈(0，
| π |
| 2 |
∴f（x）＞f（0）=0，
∴x＞sinx，则只有x=0时sin0=0，
又函数y=sinx与y=x均为奇函数，
∴在同一坐标系中，函数y=sinx的图象与函数y=x的图象只有1个公共点，命题③错误；
对于④，把函数y=3sin（2x+
| π |
| 3 |
| π |
| 6 |
得到y=3sin[2(x-
| π |
| 6 |
| π |
| 3 |
∴命题④正确．
∴正确的命题是①④．
故答案为：①④．
点评：本题考查命题的真假判断与应用，考查了与三角函数有关的函数的图象与性质，利用函数单调性判断函数
y=sinx的图象与函数y=x的图象交点是解答该题的关键，是中档题．
y=sinx的图象与函数y=x的图象交点是解答该题的关键，是中档题．
练习册系列答案
相关题目
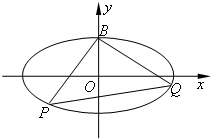已知椭圆C：
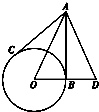如图，AB、AC为⊙O的切线，B和C是切点，延长OB到D，使BD=OB，连接AD．如果∠DAC=78°，那么∠ADO等于