题目内容
已知函数f(x)=
,请利用单调性定义判断f(x)在[1,3]上的单调性,并求函数在[1,3]上的值域.
| x2+9 |
| x |
考点:函数的最值及其几何意义,函数单调性的判断与证明,函数单调性的性质
专题:函数的性质及应用
分析:直接利用单调性定义判断函数单调性的方法,证明f(x)在[1,3]上是减函数,然后求解函数的最值.
解答:
(本小题满分14分)
解:在[1,3]上任取x1<,x2且x1<x2,…(2分)
则f(x1)-f(x2)=
-
=
…(6分)
∵1≤x1<x2≤3∴x1-x2<0,x1x2-9<0,…(8分)
∴f(x1)-f(x2)>0,∴f(x1)>f(x2)
∴f(x)是在[1,3]上的减函数.…(10分)
∴f(x)min=f(3)=6,f(x)max=f(1)=10
因此,函数在[1,3]上的值域为[6,10]…(14分)
解:在[1,3]上任取x1<,x2且x1<x2,…(2分)
则f(x1)-f(x2)=
| ||
| x1 |
| ||
| x2 |
| (x1-x2)(x1x2-9) |
| x1x2 |
∵1≤x1<x2≤3∴x1-x2<0,x1x2-9<0,…(8分)
∴f(x1)-f(x2)>0,∴f(x1)>f(x2)
∴f(x)是在[1,3]上的减函数.…(10分)
∴f(x)min=f(3)=6,f(x)max=f(1)=10
因此,函数在[1,3]上的值域为[6,10]…(14分)
点评:本题考查函数的单调性的判断与证明,单调性的应用,基本知识的考查.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案
相关题目
设全集为R,集合M={x|log2(x-1)<1},则∁RM=( )
| A、[3,+∞) |
| B、(-∞,1]∪[2,+∞) |
| C、(-∞,1]∪[3,+∞) |
| D、(-∞,0]∪[2,+∞) |
已知全集U={0,2,4,6,8,10},集合A={2,4,6},B={0,2,6,8},则CU(A∩B)为( )
| A、{0,8,10} |
| B、{0,4,8,10} |
| C、{10} |
| D、∅ |
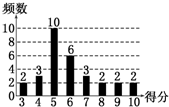 为了普及环保知识,增强环保意识,某大学随机抽取30名学生参加环保知识测试,得分(十分制)如图所示,假设得分值的中位数为me,众数为m0,平均值为
为了普及环保知识,增强环保意识,某大学随机抽取30名学生参加环保知识测试,得分(十分制)如图所示,假设得分值的中位数为me,众数为m0,平均值为. |
| x |
A、me=m0=
| ||
B、me=m0<
| ||
C、me<m0<
| ||
D、m0<me<
|