题目内容
已知点P在抛物线y2=4x上，点M在圆（x-3）2+（y-1）2=1上，点N坐标为（1，0），则|PM|+|PN|的最小值为（ ）
| A、5 | ||
| B、4 | ||
| C、3 | ||
D、
|
考点：抛物线的简单性质
专题：直线与圆,圆锥曲线的定义、性质与方程
分析：由已知可得N为抛物线y2=4x的焦点，则|PM|+|PN|的最小值等于M点到准x=-1的距离，进而根据M点在圆（x-3）2+（y-1）2=1上，可得答案
解答：
解：∵抛物线y2=4x的焦点为N（1，0），
∴当|PM|+|PN|的最小值等于M点到准x=-1的距离，
∵M点在圆（x-3）2+（y-1）2=1上，
∴M点到准x=-1的距离d等于圆心（3，1）到准线的距离4减半径1，即d=4-1=3，
故选：C
∴当|PM|+|PN|的最小值等于M点到准x=-1的距离，
∵M点在圆（x-3）2+（y-1）2=1上，
∴M点到准x=-1的距离d等于圆心（3，1）到准线的距离4减半径1，即d=4-1=3，
故选：C
点评：本题考查的知识点是抛物线的简单性质，点到直线的距离，其中将|PM|+|PN|的最小值转化为：M点到准x=-1的距离，是解答的关键．
练习册系列答案
相关题目
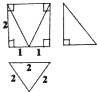
如图所示，在△ABC中，D为BC边上的一点，且BD=2DC．若某几何体的三视图如图所示，则该几何体的体积是（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知函数f（x）是定义在R上的奇函数，当x≥0时，f（x）=
（|x-a2|+|x-2a2|-3a2），若对于任意的实数x，都有f（x-1）≤f（x）成立，则实数a的取值范围是（ ）
| 1 |
| 2 |
A、[-
| ||||||||
B、[-
| ||||||||
C、[-
| ||||||||
D、[-
|
若任取x，y∈[0，1]，则点P（x，y）满足y＞
的概率为（ ）
| x |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
设a=（
）
，b=log2
，c=log23，则（ ）
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| A、a＞b＞c |
| B、c＞a＞b |
| C、a＞c＞b |
| D、c＞b＞a |
已知函数f（x）=x2+（2a-1）x-3，x∈[-2，3]．