题目内容
设锐角△ABC的内角A,B,C所对的边分别为a,b,c且acosC+
c=b.
(Ⅰ)求角A的大小;
(Ⅱ)求函数y=2sin2B+cos(
-2B)的值域.
| 1 |
| 2 |
(Ⅰ)求角A的大小;
(Ⅱ)求函数y=2sin2B+cos(
| π |
| 3 |
考点:正弦定理的应用,二倍角的余弦
专题:计算题,解三角形
分析:(Ⅰ)由正弦定理化简可求得cosA=
,从而可求角A的大小;
(Ⅱ)化简可得y=2sin2B+cos(
-2B)=sin(2B-
)+1,再求得
<2B-
<
,从而求出
<sin(2B-
)+1≤2.
| 1 |
| 2 |
(Ⅱ)化简可得y=2sin2B+cos(
| π |
| 3 |
| π |
| 6 |
| π |
| 6 |
| π |
| 6 |
| 5π |
| 6 |
| 3 |
| 2 |
| π |
| 6 |
解答:
解:(Ⅰ)△ABC中,∵acosC+
c=b,由正弦定理可得sinAcosC+
sinC=sinB
∴有2sinAcosC+sinC=2sin(A+C)
∴2sinAcosC+sinC=2sinAcosC+2cosAsinC
∴2cosAsinC=sinC,∵0<sinC<1,∴2cosA=1
∵0<A<
∴cosA=
,∴A=
(Ⅱ)y=1-cos2B+cos
cos2B+sin
sin2B=
sin2B-
cos2B+1=sin(2B-
)+1
∵△ABC为锐角三角形
∴
∴
<B<
∴
<2B-
<
∴
<sin(2B-
)≤1
∴
<sin(2B-
)+1≤2
| 1 |
| 2 |
| 1 |
| 2 |
∴有2sinAcosC+sinC=2sin(A+C)
∴2sinAcosC+sinC=2sinAcosC+2cosAsinC
∴2cosAsinC=sinC,∵0<sinC<1,∴2cosA=1
∵0<A<
| π |
| 2 |
∴cosA=
| 1 |
| 2 |
| π |
| 3 |
(Ⅱ)y=1-cos2B+cos
| π |
| 3 |
| π |
| 3 |
| ||
| 2 |
| 1 |
| 2 |
| π |
| 6 |
∵△ABC为锐角三角形
∴
|
∴
| π |
| 6 |
| π |
| 2 |
∴
| π |
| 6 |
| π |
| 6 |
| 5π |
| 6 |
∴
| 1 |
| 2 |
| π |
| 6 |
∴
| 3 |
| 2 |
| π |
| 6 |
点评:本题主要考察了正弦定理的应用,二倍角的余弦,属于中档题.

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案
相关题目
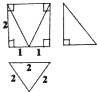
某几何体的三视图如图所示,则该几何体的体积是( )

A、
| ||||
B、
| ||||
C、
| ||||
D、
|
设△ABC的角A,B,C的对边分别为a,b,c,且a,b,c成等差数列.给出以下四个结论:
①b2≥ac;②
+
≥
; ③b2≤
; ④B∈(0,
]
其中正确结论的个数为( )
①b2≥ac;②
| 1 |
| a |
| 1 |
| c |
| 2 |
| b |
| a2+c2 |
| 2 |
| π |
| 3 |
其中正确结论的个数为( )
| A、4 | B、3 | C、2 | D、1 |
设f(x)=|lg(x-1)|,若0<a<b,且f(a)=f(b),则ab的取值范围是( )
| A、[1,2] |
| B、(1,2) |
| C、(4,+∞) |
| D、(2,+∞) |
 已知函数f(x)=x2+(2a-1)x-3,x∈[-2,3].
已知函数f(x)=x2+(2a-1)x-3,x∈[-2,3].