题目内容
已知函数f(x+1)=x2+2x-5,则f(x)的解析式为( )
| A、f(x)=x2 |
| B、f(x)=x2-6 |
| C、f(x)=x2+6 |
| D、f(x)=x2+6x |
考点:函数解析式的求解及常用方法
专题:函数的性质及应用
分析:由已知中f(x+1)=x2+2x-5,将式子右边凑配成a(x+1)2+b(x+1)+c的形式,进而将(x+1)全部替换成x后,即可得到答案.
解答:
解:∵f(x+1)=x2+2x-5
=(x+1)2-6
∴f(x)=x2-6
故选:B.
=(x+1)2-6
∴f(x)=x2-6
故选:B.
点评:本题考查的知识点是函数解析式的求解及其常用方法,本题使用的凑配法,是已知复合函数解析式及内函数的解析式,求外函数解析式时常用的方法,请熟练掌握.

练习册系列答案
相关题目
已知双曲线
-y2=1(a>0)的实轴长2,则该双曲线的离心率为( )
| x2 |
| a |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
设z=x+y,其中实数x,y满足
若z的最大值为12,则z的最小值为( )
|
| A、-3 | B、3 | C、-6 | D、6 |
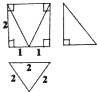
某几何体的三视图如图所示,则该几何体的体积是( )

A、
| ||||
B、
| ||||
C、
| ||||
D、
|
若任取x,y∈[0,1],则点P(x,y)满足y>
的概率为( )
| x |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|