题目内容
已知数列{an}的前n项和Sn=n2-4n+2.
(1)求{an}的通项an;
(2)已知Tn=|a1|+|a2|+…+|an|,求Tn.
(1)求{an}的通项an;
(2)已知Tn=|a1|+|a2|+…+|an|,求Tn.
考点:数列的求和
专题:综合题,等差数列与等比数列
分析:(1)当n=1时,a1=S1,当n≥2时,an=Sn-Sn-1,求出数列的通项公式;
(2)利用通项公式,确定项的取值符号,然后去掉绝对值,再利用等差数列的前n项和公式即可得出.
(2)利用通项公式,确定项的取值符号,然后去掉绝对值,再利用等差数列的前n项和公式即可得出.
解答:
解:(1)当n=1时,a1=S1=1-4+2=-1;
当n≥2时,an=Sn-Sn-1=n2-4n+2-[(n-1)2-4(n-1)+2]=2n-5.
∴an=
(2)当n=1,2时,a1=-1<0,a2=-1<0,
∴n≤2,Tn=-Sn=-n2+4n-2;
当n≥3时,an>0.
∴Tn=|a1|+|a2|+…+|an|=-a1-a2+a3+a4+…+an=4+n2-4n+2=n2-4n+6.
故选A.
当n≥2时,an=Sn-Sn-1=n2-4n+2-[(n-1)2-4(n-1)+2]=2n-5.
∴an=
|
(2)当n=1,2时,a1=-1<0,a2=-1<0,
∴n≤2,Tn=-Sn=-n2+4n-2;
当n≥3时,an>0.
∴Tn=|a1|+|a2|+…+|an|=-a1-a2+a3+a4+…+an=4+n2-4n+2=n2-4n+6.
故选A.
点评:本题考查了等差数列的通项公式和前n项和公式及含绝对值符号的数列求和,由通项公式得出从哪一项开始大于0是解题的关键,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
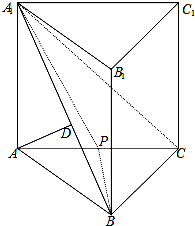 如图,在直三棱柱ABC=A1B1C1中,AD⊥平面A1BC,其垂足D落在直线A1B上.
如图,在直三棱柱ABC=A1B1C1中,AD⊥平面A1BC,其垂足D落在直线A1B上.