题目内容
某校高二的一个班的一次数学测试成绩的茎叶图图1和频率分布直方图图2都受到不同程度的破坏,但可见部分如下,据此解答如下问题:
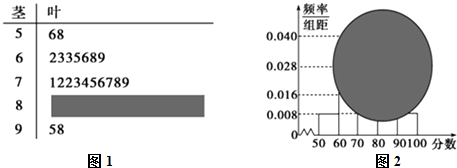
(Ⅰ)求分数在[50,60)的频率及全班人数;
(Ⅱ)求分数在[80,90)之间的频数,并计算频率分布直方图中[80,90)间的矩形的高;
(Ⅲ)试用此频率分布直方图估计这组数据的众数和平均数.

(Ⅰ)求分数在[50,60)的频率及全班人数;
(Ⅱ)求分数在[80,90)之间的频数,并计算频率分布直方图中[80,90)间的矩形的高;
(Ⅲ)试用此频率分布直方图估计这组数据的众数和平均数.
考点:茎叶图,频率分布直方图
专题:概率与统计
分析:(Ⅰ)分数在[50,60)的频率为0.008×10=0.08,由茎叶图知:分数在[50,60)之间的频数为2,由此能求出全班人数.
(Ⅱ)分数在[80,90)之间的频数为25-2-7-10-2=4,由此能求出频率分布直方图中[80,90)间的矩形的高.
(Ⅲ)分数在[60,70)之间的频率为:
;分数在[70,80)之间的频率为:
;分数在[90,100)之间的频率为:
.由此能用此频率分布直方图估计这组数据的众数和平均数.
(Ⅱ)分数在[80,90)之间的频数为25-2-7-10-2=4,由此能求出频率分布直方图中[80,90)间的矩形的高.
(Ⅲ)分数在[60,70)之间的频率为:
| 7 |
| 25 |
| 10 |
| 25 |
| 2 |
| 25 |
解答:
解:(Ⅰ)分数在[50,60)的频率为0.008×10=0.08,
由茎叶图知:分数在[50,60)之间的频数为2,
所以全班人数为
=25.…(4分)
(Ⅱ)分数在[80,90)之间的频数为25-2-7-10-2=4,
频率分布直方图中[80,90)间的矩形的高为
÷10=0.016.…(7分)
(Ⅲ)分数在[60,70)之间的频率为:
;
分数在[70,80)之间的频率为:
;
分数在[90,100)之间的频率为:
,
所以分数在[70,80)之间对应的矩形最高,这组数据的众数为75.…(10分)
平均数为:55×
+65×
+75×
+85×
+95×
=73.8…(12分)
由茎叶图知:分数在[50,60)之间的频数为2,
所以全班人数为
| 2 |
| 0.08 |
(Ⅱ)分数在[80,90)之间的频数为25-2-7-10-2=4,
频率分布直方图中[80,90)间的矩形的高为
| 4 |
| 25 |
(Ⅲ)分数在[60,70)之间的频率为:
| 7 |
| 25 |
分数在[70,80)之间的频率为:
| 10 |
| 25 |
分数在[90,100)之间的频率为:
| 2 |
| 25 |
所以分数在[70,80)之间对应的矩形最高,这组数据的众数为75.…(10分)
平均数为:55×
| 2 |
| 25 |
| 7 |
| 25 |
| 10 |
| 25 |
| 4 |
| 25 |
| 2 |
| 25 |
点评:本题考查茎叶图和频率分布直方图的应用,解题时要认真审题,是基础题.

练习册系列答案
相关题目
函数f(x)=sin(2x+φ)(|x|<π)的图象向左平移
个单位后关于原点对称,则函数f(x)在[0,
]上的最小值为( )
| π |
| 6 |
| π |
| 2 |
A、-
| ||||
B、-
| ||||
C、
| ||||
D、
|
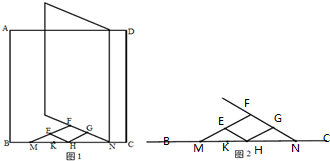 如图1是某窗户的窗扣示意图,图2是其俯视图,其中点E、F、G、M、K是固定点,点H是窗沿糟内可滑动点,点N是窗户下边沿延长线与窗沿的交点,窗户打开时,点H、N向点K移动,当点H移至点K时,不能再往左移动,此时窗户最大打开,窗户关闭时,点H、N向点C移动,当点N移动至点C时,点E、F、G落在BC上窗户刚好全部关闭.在窗户打开与关闭的过程中,四边形EFGH始终保持平行四边形的形状,现测得BM=18cm,MK=12cm,ME=EF,FG=GN,且HE=6cm,HG=10cm;
如图1是某窗户的窗扣示意图,图2是其俯视图,其中点E、F、G、M、K是固定点,点H是窗沿糟内可滑动点,点N是窗户下边沿延长线与窗沿的交点,窗户打开时,点H、N向点K移动,当点H移至点K时,不能再往左移动,此时窗户最大打开,窗户关闭时,点H、N向点C移动,当点N移动至点C时,点E、F、G落在BC上窗户刚好全部关闭.在窗户打开与关闭的过程中,四边形EFGH始终保持平行四边形的形状,现测得BM=18cm,MK=12cm,ME=EF,FG=GN,且HE=6cm,HG=10cm;