题目内容
双曲线2x2-y2=-1的离心率为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
考点:双曲线的简单性质
专题:计算题,圆锥曲线的定义、性质与方程
分析:把双曲线的方程化为标准形式,求出a、b、c 的值,即得离心率的值.
解答:
解:双曲线2x2-y2=-1化为标准形式为y2-
=1,
∴a=1,b=
,
∴c=
=
,
∴e=
=
,
故选:A.
| x2 | ||
|
∴a=1,b=
| ||
| 2 |
∴c=
| a2+b2 |
| ||
| 2 |
∴e=
| c |
| a |
| ||
| 2 |
故选:A.
点评:本题考查双曲线的标准方程,以及双曲线的简单性质的应用,把双曲线的方程化为标准形式是解题的突破口.

练习册系列答案
 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案
相关题目
设x、y满足约束条件
,若x2+y2≥a恒成立,则实数a的最大值为( )
|
A、
| ||
B、
| ||
C、
| ||
D、
|
 学校为了调查学生在课外读物方面的支出情况,将支出分区间[20,30)、[30,40)、[40,50)、[50,60)进行统计,现抽出了一个容量为n的样本,其频率分布直方图如图所示,其中支出在[50,60)元的同学有24人,则n的值为( )
学校为了调查学生在课外读物方面的支出情况,将支出分区间[20,30)、[30,40)、[40,50)、[50,60)进行统计,现抽出了一个容量为n的样本,其频率分布直方图如图所示,其中支出在[50,60)元的同学有24人,则n的值为( )| A、80 | B、800 |
| C、72 | D、720 |
过双曲线
-
=1(a>0,b>0)的一个焦点作实轴的垂线,交双曲线于A,B两点,若线段AB的长度恰等于焦距,则双曲线的离心率为( )
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 如图所示,矩形O′A′B′C′是水平放置一个平面图形的直观图,其中O′A′=6,O′C′=2,则原图形是( )
如图所示,矩形O′A′B′C′是水平放置一个平面图形的直观图,其中O′A′=6,O′C′=2,则原图形是( )| A、正方形 | B、矩形 |
| C、菱形 | D、一般的平行四边形 |
已知变量x,y满足约束条件
,则z=4x+y的最小值为( )
|
| A、55 | B、-55 | C、5 | D、-5 |
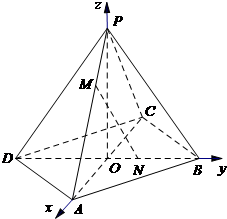 如图,在空间直角坐标系O-xyz中,正四棱锥P-ABCD的侧棱长与底边长都为
如图,在空间直角坐标系O-xyz中,正四棱锥P-ABCD的侧棱长与底边长都为