题目内容
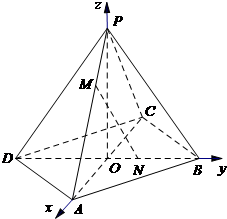如图，在空间直角坐标系O-xyz中，正四棱锥P-ABCD的侧棱长与底边长都为3| 2 |
| PM |
| PA |
| BN |
| BD |
| 1 |
| 3 |
（1）求证：MN⊥AD；
（2）求MN与平面PAD所成角的正弦值．
考点：直线与平面所成的角
专题：综合题,空间位置关系与距离,空间角
分析：（1）求出
=（-1，1，-2），
=（-3，-3，0），证明
•
=3-3+0=0，可得
⊥
，即可证明MN⊥AD；
（2）求出平面PAD的法向量，利用向量的夹角公式，即可求MN与平面PAD所成角的正弦值．
| MN |
| AD |
| MN |
| AD |
| MN |
| AD |
（2）求出平面PAD的法向量，利用向量的夹角公式，即可求MN与平面PAD所成角的正弦值．
解答：
（1）证明：由题意，A（3，0，0），D（0，-3，0），M（1，0，2），N（0，1，0），则
=（-1，1，-2），
=（-3，-3，0）．
∴
•
=3-3+0=0，
∴
⊥
，
∴MN⊥AD；
（2）解：∵P（0，0，3），A（3，0，0），D（0，-3，0），
∴
=（3，0，-3），
=（-3，-3，0），
设平面PAD的法向量为
=（x，y，z），则
，
∴可取
=（1，-1，1），
∵
=（-1，1，-2），
∴MN与平面PAD所成角的正弦值为|
|=|
|=
．
| MN |
| AD |
∴
| MN |
| AD |
∴
| MN |
| AD |
∴MN⊥AD；
（2）解：∵P（0，0，3），A（3，0，0），D（0，-3，0），
∴
| PA |
| AD |
设平面PAD的法向量为
| n |
|
∴可取
| n |
∵
| MN |
∴MN与平面PAD所成角的正弦值为|
| ||||
|
|
| -1-1-2 | ||||
|
2
| ||
| 3 |
点评：本题考查线线垂直，考查线面角，考查向量知识的运用，正确求出平面的法向量是关键．
练习册系列答案
相关题目
双曲线2x2-y2=-1的离心率为（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、
|