题目内容
已知：三条抛物线y=ax2+2bx+c，y=bx2+2cx+a，y=cx2+2ax+b（a，b，c是不为0，且互不相等的不实数），证明此三条抛物线至少有一条与x轴有两个交点．
考点：二次函数的性质
专题：函数的性质及应用
分析：假设这三条抛物线没有一条与x轴有两个交点，则它们的判别式都小于或等于零，求得（a-b）2+（b-c）2+（a-c）2≤0 ①．由a，b，c是不为0，且互不相等的不实数，可得 （a-b）2+（b-c）2+（a-c）2＞0，这与①相矛盾，故假设不成立，原命题得证．
解答：
证明：用反证法，假设这三条抛物线没有一条与x轴有两个交点，则它们的判别式都小于或等于零，
即 4b2-4ac≤0，且 4c2-4ab≤0，且4a2-4bc≤0，
所以，（4b2-4ac）+（4c2-4ab）+（4a2-4bc）≤0，
即 2（a2+b2+c2）-2ab-2bc-2ac≤0，即 （a-b）2+（b-c）2+（a-c）2≤0 ①．
因为a，b，c是不为0，且互不相等的不实数，
所以，（a-b）2+（b-c）2+（a-c）2＞0，这与①相矛盾，故假设不成立，
所以原命题成立．
即 4b2-4ac≤0，且 4c2-4ab≤0，且4a2-4bc≤0，
所以，（4b2-4ac）+（4c2-4ab）+（4a2-4bc）≤0，
即 2（a2+b2+c2）-2ab-2bc-2ac≤0，即 （a-b）2+（b-c）2+（a-c）2≤0 ①．
因为a，b，c是不为0，且互不相等的不实数，
所以，（a-b）2+（b-c）2+（a-c）2＞0，这与①相矛盾，故假设不成立，
所以原命题成立．
点评：本题主要考查二次函数的性质，用反证法证明数学命题，属于基础题．
练习册系列答案
名校课堂系列答案
相关题目
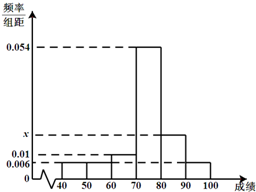某班50位学生期中考试数学成绩的频率分布直方图如图所示，其中成绩分组区间是：[40，50）、[50，60）、[60，70）、[70，80）、[80，90）、[90，100]．
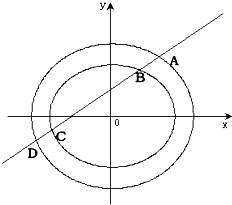已知椭圆C1：