题目内容
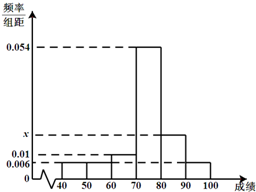 某班50位学生期中考试数学成绩的频率分布直方图如图所示,其中成绩分组区间是:[40,50)、[50,60)、[60,70)、[70,80)、[80,90)、[90,100].
某班50位学生期中考试数学成绩的频率分布直方图如图所示,其中成绩分组区间是:[40,50)、[50,60)、[60,70)、[70,80)、[80,90)、[90,100].(1)求图中x的值;
(2)从成绩不低于80分的学生中随机选取2人,该2人中成绩在90分以上(含90分)的人数记为ξ,求ξ的分布列.
考点:离散型随机变量及其分布列,频率分布直方图
专题:概率与统计
分析:(Ⅰ)由频率分布直方图能求出图中x的值.
(Ⅱ)由题意知ξ的取值为0、1、2.分别求出相应的概率,由此能求出ξ的分布列.
(Ⅱ)由题意知ξ的取值为0、1、2.分别求出相应的概率,由此能求出ξ的分布列.
解答:
(Ⅰ)由频率分布直方图得:
(0.006×3+0.01+0.054+x)×10=1,
解得x=0.018.
(Ⅱ)分数在[80,90)、[90,100]的人数分别是:
50×0.018×10=9人、50×0.006×10=3人.
所以ξ的取值为0、1、2.
P(ξ=0)=
=
=
,
P(ξ=1)=
=
=
,
P(ξ=2)=
=
=
,
所以ξ的分布列为:
(0.006×3+0.01+0.054+x)×10=1,
解得x=0.018.
(Ⅱ)分数在[80,90)、[90,100]的人数分别是:
50×0.018×10=9人、50×0.006×10=3人.
所以ξ的取值为0、1、2.
P(ξ=0)=
| ||||
|
| 36 |
| 66 |
| 6 |
| 11 |
P(ξ=1)=
| ||||
|
| 27 |
| 66 |
| 9 |
| 22 |
P(ξ=2)=
| ||||
|
| 3 |
| 66 |
| 1 |
| 22 |
所以ξ的分布列为:
| ξ | 0 | 1 | 2 | ||||||
| P |
|
|
|
点评:本题考查频率分布直方图的应用,考查离散型随机变量的分布列和数学期望的求法,是中档题,解题时要认真审题,在历年高考中都是必考题型.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案
相关题目
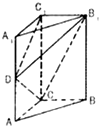 如图,直三棱柱ABC-A1B1C1中AA1=2AC=2BC,D是AA1的中点,CD⊥B1D.
如图,直三棱柱ABC-A1B1C1中AA1=2AC=2BC,D是AA1的中点,CD⊥B1D. 已知连续型随机变量ξ的概率密度函数f(x)=
已知连续型随机变量ξ的概率密度函数f(x)=