题目内容
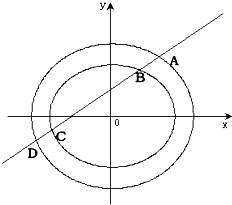已知椭圆C1：| x2 |
| a2 |
| y2 |
| b2 |
| 5 |
| x2 |
| 5 |
| y2 |
| 4 |
（Ⅰ）求线段BC的长（用k和a表示）；
（Ⅱ）是否存在这样的直线L，使线段AB、BC、CD的长按此顺序构成一个等差数列．请说明详细的理由．
考点：直线与圆锥曲线的综合问题
专题：圆锥曲线中的最值与范围问题
分析：（Ⅰ）联立
，得（k2a2+b2）x2+2k2a2x2+k2a2-a2b2=0，由此能求出线段BC的长．
（Ⅱ）由（I）知，AD=
，线段AB、BC、CD构成一个等差数列，得2BC=AB+CD，故3BC=AD，由此能求出存在这样的直线L，使线段AB、BC、CD的长按此顺序构成一个等差数列．
|
（Ⅱ）由（I）知，AD=
8
| ||
| 5k2+4 |
解答：
解：（Ⅰ）联立
，
得（k2a2+b2）x2+2k2a2x2+k2a2-a2b2=0
所以BC=
=
．
（Ⅱ）由（I）知，AD=
，
线段AB、BC、CD构成一个等差数列，
可得2BC=AB+CD，故3BC=AD，
3•
=
，
k2=
=
≥0，
即：
≥0．
由于a＞1，故
＜a＜
．
所以，当
＜a＜
时，
存在这样的直线L，使线段AB、BC、CD的长按此顺序构成一个等差数列．
|
得（k2a2+b2）x2+2k2a2x2+k2a2-a2b2=0
所以BC=
| 2ab2(k2+1) |
| k2a2+b2 |
| 2a(a2-1)(k2+1) |
| k2a2+a2-1 |
（Ⅱ）由（I）知，AD=
8
| ||
| 5k2+4 |
线段AB、BC、CD构成一个等差数列，
可得2BC=AB+CD，故3BC=AD，
3•
| 2a(a2-1)(k2+1) |
| k2a2+a2-1 |
8
| ||
| 5k2+4 |
k2=
4(a2-1)(3a-
| ||
a(15a2-4
|
4(a2-1)(3a-
| ||||
a(3a+
|
即：
3a-
| ||
5a-3
|
由于a＞1，故
3
| ||
| 5 |
| 5 |
所以，当
3
| ||
| 5 |
| 5 |
存在这样的直线L，使线段AB、BC、CD的长按此顺序构成一个等差数列．
点评：本题考查线段长的求法，考查满足条件的线段是否存在的判断与求法，是中档题，解题时要注意函数与方程思想的合理运用．
练习册系列答案
阅读快车系列答案
相关题目
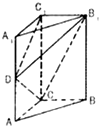如图，直三棱柱ABC-A1B1C1中AA1=2AC=2BC，D是AA1的中点，CD⊥B1D．
已知连续型随机变量ξ的概率密度函数f（x）=