题目内容
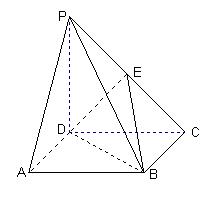
如图,四棱锥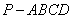 的底面
的底面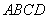 是正方形,棱
是正方形,棱 底面
底面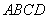 ,
,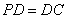 =1,
=1,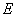 是
是 的中点.
的中点.
(1)证明平面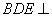 平面
平面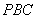 ;
;
(2)求二面角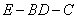 的余弦值.
的余弦值.
证明:(1) ∵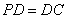 ,
,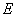 是
是 的中点, ∴
的中点, ∴ .
.
∵ 底面
底面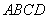 ,∴
,∴ .又由于
.又由于 ,
, ,
,
故 底面
底面 ,
,
所以有 .又由题意得
.又由题意得 ,故
,故 .
.
于是,由 ,
, ,
, 可得
可得 底面
底面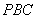 .
.
故可得平面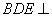 平面
平面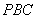

(2)取CD的中点F,连接AC与BD,交点为M,取DM的中点N,连接EN,FN,易知 为二面角
为二面角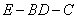 的平面角,又
的平面角,又 ,
, ,由勾股定理得
,由勾股定理得 ,在
,在 中,
中,
所以二面角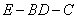 的余弦值为
的余弦值为

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
已知函数f(x)在R上满足f(x)=2f(2﹣x)﹣x2+8x﹣8,则曲线y=f(x)在点 (1,f(1))处切线的斜率是 ( )
|
| A. | 2 | B. | 1 | C. | 3 | D. | ﹣2 |
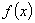 满足
满足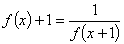 ,当
,当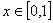 时,
时,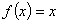 ,若在区间
,若在区间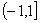 上,
上,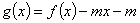 有两个零点,则实数
有两个零点,则实数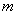 的取值范围是( )
的取值范围是( )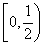 B.
B. C.
C.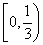 D.
D.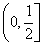
 关于原点
关于原点 对称的圆的方程为( )
对称的圆的方程为( ) B.
B.
 D.
D.
 ”是“
”是“ ”的充分不必要条件,则实数
”的充分不必要条件,则实数 的取值范围是___________
的取值范围是___________  ,则
,则 ( )
( ) B.
B. C .
C . D.
D.
 为
为 上的可导函数,当
上的可导函数,当 时,
时, ,则关于的函数
,则关于的函数 的零点个数为( )
的零点个数为( )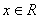 时,函数
时,函数 始终满足
始终满足 ,则函数
,则函数 的图象大致为( )
的图象大致为( )
 是两条不同的直线,
是两条不同的直线, 是三个不同的平面,下列四个命题中假命题的是( )
是三个不同的平面,下列四个命题中假命题的是( )  则
则 B.若
B.若 则
则
 则
则 D.若
D.若 ,则
,则