题目内容
20.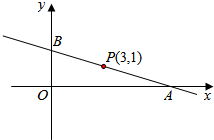 过点P(3,1)作直线l.
过点P(3,1)作直线l.(Ⅰ)当直线l的倾斜角α为135°时,求直线l的方程;
(Ⅱ)当直线l在两坐标轴截距相等时,求直线l的方程.
分析 (Ⅰ)根据已知求出直线斜率,进而可得直线的点斜式方程;
(Ⅱ)当直线l在两坐标轴截距相等时,直线过原点或斜率为-1,进而得到直线方程.
解答  解:(Ⅰ)根据题意,得k=tanα=tan135°=-1.
解:(Ⅰ)根据题意,得k=tanα=tan135°=-1.
故由点斜式得直线l的方程为y-1=-(x-3),
即x+y-4=0.
(Ⅱ)设直线l分别与x轴、y轴相交于A(a,0),B(0,a)两点,
当a≠0时,直线l的方程为x+y=a,
因为点P(3,1)在直线l上,所以a=3+1=4.
故直线l的方程为x+y-4=0,
当a=0时,直线l的方程为y=kx,
因为点P(3,1)在直线l上,所以1=3k.
解得$k=\frac{1}{3}$.
故直线l的方程为$y=\frac{1}{3}x$.
综上所述,直线l的方程为$y=\frac{1}{3}x$或x+y-4=0.
点评 本题考查的知识点是直线的斜率,直线的点斜式方程,分类讨论思想,难度中档.

练习册系列答案
相关题目
11.记方程①x2+a1x+1=0,②x2+a2x+1=0,③x2+a3x+1=0,其中a1,a2,a3是正实数,当a1,a2,a3成等比数列,下列选项中,当方程③有实根时,能推出的是( )
| A. | 方程①有实根或方程②无实根 | B. | 方程①有实根或方程②有实根 | ||
| C. | 方程①无实根或方程②无实根 | D. | 方程①无实根或方程②有实根 |
9.α是第四象限角,P($\sqrt{5}$,x)为其终边上一点,且sinα=$\frac{\sqrt{2}}{4}$x,则cosα的值为( )
| A. | $\frac{\sqrt{10}}{4}$ | B. | $\frac{\sqrt{6}}{4}$ | C. | $\frac{\sqrt{2}}{4}$ | D. | -$\frac{\sqrt{10}}{4}$ |
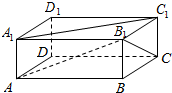 如图所示,ABCD-A1B1C1D1是长方体,AA1=a,∠BAB1=∠B1A1C1=30°,则AB与A1C1所成的角为30°,AA1与B1C所成的角为45°.
如图所示,ABCD-A1B1C1D1是长方体,AA1=a,∠BAB1=∠B1A1C1=30°,则AB与A1C1所成的角为30°,AA1与B1C所成的角为45°.