题目内容
12.设函数f(x)在R上存在导数f′(x),?x∈R,有f(-x)+f(x)=x2,在(0,+∞)上f′(x)<x,若f(2-m)-f(m)>2-2m,则实数m的取值范围为(1,+∞).分析 利用构造法$g(x)=f(x)-\frac{1}{2}{x^2}$,推出g(x)为奇函数,判断g(x)的单调性,然后推出不等式得到结果.
解答 解:∵f(-x)+f(x)=x2,∴f(x)-x2+f(-x)=0
∵$g({-x})+g(x)=f({-x})-\frac{1}{2}{x^2}+f(x)-\frac{1}{2}{x^2}=0$
∴函数g(x)为奇函数.
∵x∈(0,+∞)时,g′(x)=f′(x)-x<0,
故函数g(x)在(0,+∞)上是减函数,
故函数g(x)在(-∞,0)上也是减函数,
由f(0)=0,可得g(x)在R上是减函数.
f(2-m)-f(m)>2-2m等价于$f({2-m})-\frac{{{{({2-m})}^2}}}{2}>f(m)-\frac{m^2}{2}$,
即g(2-m)<g(m),∴2-m<m,解得m>1
故答案为:(1,+∞).
点评 本题考查函数奇偶性、单调性、导数的综合应用,考查分析问题解决问题的能力,难度比较大.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
2.i是虚数单位.已知复数$Z=\frac{1+3i}{3+i}+{({1+i})}^2$,则复数Z对应点落在( )
| A. | 第四象限 | B. | 第三象限 | C. | 第二象限 | D. | 第一象限 |
4.已知-9,a1,a2,-1成等差数列,-9,b1,b2,b3,-1成等比数列,则b2(a1+a2)等于( )
| A. | 30 | B. | -30 | C. | ±30 | D. | 15 |
2.已知几何体的三视图(如图),则该几何体的表面积为( )
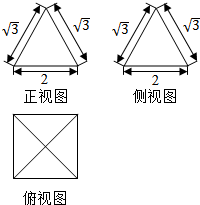

| A. | $4\sqrt{2}$ | B. | $4\sqrt{3}$ | C. | 4$\sqrt{2}$+4 | D. | 4$\sqrt{3}$+4 |
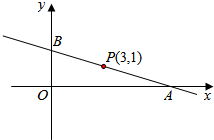 过点P(3,1)作直线l.
过点P(3,1)作直线l.