题目内容
8.S国政府为了保护本国产业,决定对从外国进来的产品加收附加税.已知进口的产品在当地的市场零售价是每个500元,每年可以销售40万个,若政府征收的附加税率为每百个t元时,则每年销售将减少1.6t万个.①将税金收入表示为征收附加税率的函数;
②若每年征收附加税金不低于1200万,那么每年征收的附加税率要控制在什么范囤.
分析 (1)设出每年国内的销售量x万件,则x=40-1.6t,代入征收附加税金y=500x•t%可得征收附加税率的函数;
(2)直接由500×(40-1.6t)×t%≥1200求解不等式得答案
解答 解:(1)设每年国内销量为x万件,
则销售收入为每年500x万元,征收附加税金为y=500x•t%,这里x=40-1.6t,
则所求函数关系为y=500×(40-1.6t)×t%;
(2)依题意,500×(40-1.6t)×t%≥1200,即t2-25t+150≤0,
解得10≤t≤15.
即税率应控制在10%到15%之间
点评 本题考查了函数模型的选择及应用,考查了数学建模思想方法,关键是对题意得理解,是中档题.

练习册系列答案
相关题目
19.执行下面的程序框图,则输出的m的值为( )


| A. | 2 | B. | 4 | C. | 5 | D. | 9 |
16.已知函数f(x)的义域为D.对于任意的x1∈D,存在唯一的x2∈D,使得$\sqrt{f({x_1})•f({x_2})}=M$成立,则称函数f(x)在D上的几何平均数为M.已知函数g(x)=3x+1(x∈[0,1]),则g(x)在区间[0,1]上的几何平均数为( )
| A. | 1 | B. | $\sqrt{2}$ | C. | 2 | D. | 4 |
18.某研究机构对高二学生的记忆力x和判断力y进行统计分析,得下表数据
(1)请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$;
(2)试根据(1)求出的线性回归方程,预测记忆力为9的同学的判断力.
($\widehat{b}=\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$,$\widehat{a}=\overline{y}-\widehat{b}\overline{x}$)
| x | 6 | 8 | 10 | 12 |
| y | 3 | 4 | 6 | 7 |
(2)试根据(1)求出的线性回归方程,预测记忆力为9的同学的判断力.
($\widehat{b}=\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$,$\widehat{a}=\overline{y}-\widehat{b}\overline{x}$)
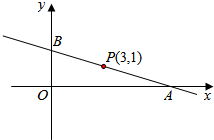 过点P(3,1)作直线l.
过点P(3,1)作直线l.