题目内容
5.曲线y=x2和直线x=0,x=1,y=$\frac{1}{4}$ 所围成的图形的面积为$\frac{1}{4}$.分析 求出曲线y=x2和直线:x=1的交点为(1,1),和直线y=$\frac{1}{4}$的一个交点为($\frac{1}{2}$,$\frac{1}{4}$),由此用定积分计算公式加以运算即可得到本题答案.
解答 解:∵曲线y=x2和直线:x=1的交点为(1,1),和直线y=$\frac{1}{4}$的一个交点为($\frac{1}{2}$,$\frac{1}{4}$)
∴曲线y=x2和直线x=0,x=1,y=$\frac{1}{4}$ 所围成的图形的面积为S=${∫}_{0}^{\frac{1}{2}}$($\frac{1}{4}-{x}^{2}$)dx+${∫}_{\frac{1}{2}}^{1}({x}^{2}-\frac{1}{4})$dx=($\frac{1}{4}$x-$\frac{1}{3}$x3)${|}_{0}^{\frac{1}{2}}$+($\frac{1}{3}$x3-$\frac{1}{4}$x)${|}_{\frac{1}{2}}^{1}$=$\frac{1}{4}$.
故答案为:$\frac{1}{4}$.
点评 本题求两条曲线围成的曲边图形的面积,着重考查了定积分的几何意义和积分计算公式等知识,属于基础题.

练习册系列答案
相关题目
15.已知某几何体的正视图和侧视图均如图所示,给出下列5个图形:

其中可以作为该几何体的俯视图的图形个数是( )

其中可以作为该几何体的俯视图的图形个数是( )
| A. | 5个 | B. | 4个 | C. | 3个 | D. | 2个 |
16.已知函数f(x)的义域为D.对于任意的x1∈D,存在唯一的x2∈D,使得$\sqrt{f({x_1})•f({x_2})}=M$成立,则称函数f(x)在D上的几何平均数为M.已知函数g(x)=3x+1(x∈[0,1]),则g(x)在区间[0,1]上的几何平均数为( )
| A. | 1 | B. | $\sqrt{2}$ | C. | 2 | D. | 4 |
10.已知x,y满足约束条件$\left\{\begin{array}{l}y≤x\\ x+y≤1\\ y≥-1\end{array}\right.$,则z=2x-3y的最大值为( )
| A. | $\frac{1}{2}$ | B. | 1 | C. | 7 | D. | $-\frac{1}{2}$ |
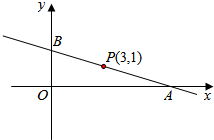 过点P(3,1)作直线l.
过点P(3,1)作直线l.