题目内容
15.已知xn-1=$\frac{1}{1+\frac{1}{{x}_{n}}}$(n为1,2,3).(1)当x1=a时,求x2012的值;
(2)当x1=b时,求x1×x2+x2×x3+…+x2010×x2011+x2011×x2012的值.
分析 (1)通过对xn-1=$\frac{1}{1+\frac{1}{{x}_{n}}}$变形可知xn=$\frac{{x}_{n-1}}{1-{x}_{n-1}}$,通过计算出前几项的值猜想通项公式并利用数学归纳法证明猜想,进而可得结论;
(2)通过(1)裂项可知xn×xn+1=b[-$\frac{1}{1-(n-1)b}$+$\frac{1}{1-nb}$],进而并项相加即得结论.
解答 解:(1)∵xn-1=$\frac{1}{1+\frac{1}{{x}_{n}}}$(n为1,2,3),
∴xn=$\frac{{x}_{n-1}}{1-{x}_{n-1}}$(n为1,2,3),
∵x1=a,∴a≠1,
∴x2=$\frac{a}{1-a}$,x3=$\frac{\frac{a}{1-a}}{1-\frac{a}{1-a}}$=$\frac{a}{1-2a}$,x4=$\frac{\frac{a}{1-2a}}{1-\frac{a}{1-2a}}$=$\frac{a}{1-3a}$,
猜想:xn=$\frac{a}{1-(n-1)a}$.
下面用数学归纳法来证明:
①当n=1时,显然成立;
②假设当n=k(k≥2)时命题成立,
则xk+1=$\frac{{x}_{k}}{1-{x}_{k}}$=$\frac{\frac{a}{1-(k-1)a}}{1-\frac{a}{1-(k-1)a}}$=$\frac{1}{1-ka}$,即当n=k+1时命题成立;
由①、②可知xn=$\frac{a}{1-(n-1)a}$.
于是x2012=$\frac{a}{1-2011a}$;
(2)由(1)可知:当x1=b(显然b≠1)时xn=$\frac{b}{1-(n-1)b}$,
∴xn×xn+1=$\frac{b}{1-(n-1)b}$•$\frac{b}{1-nb}$=b[-$\frac{1}{1-(n-1)b}$+$\frac{1}{1-nb}$],
于是x1×x2+x3×x4+…+x2010×x2011+x2011×x2012
=b[(-1+$\frac{1}{1-b}$)+(-$\frac{1}{1-b}$+$\frac{1}{1-2b}$)+…+(-$\frac{1}{1-2009b}$+$\frac{1}{1-2010b}$)]
=b(-1+$\frac{1}{1-2010b}$)
=$\frac{2010{b}^{2}}{1-2010b}$.
点评 本题考查数列的通项及前n项和,考查运算求解能力,裂项求和是解决本题的关键,注意解题方法的积累,属于中档题.

| A. | 1 | B. | $\frac{1}{2}$ | ||
| C. | 0 | D. | 随m,n的变化而变化 |
| A. | 30 | B. | -30 | C. | ±30 | D. | 15 |
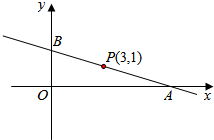 过点P(3,1)作直线l.
过点P(3,1)作直线l.