题目内容
10.过椭圆$\frac{{x}^{2}}{2}+{y}^{2}$=1的左焦点F1作倾斜角$\frac{π}{4}$为的线直线交椭圆于A,B两点,F2是右焦点,求△ABF2的面积.分析 首先根据已知条件建立方程组,通过韦达定理结合,利用弦长公式,求出|AB|.通过点到直线的距离求解三角形的高,然后求解三角形的面积.
解答 解:椭圆$\frac{{x}^{2}}{2}+{y}^{2}$=1的左焦点F1(-1,0),倾斜角为$\frac{π}{4}$的直线l的斜率为:k=1
则:直线l的方程为:y=x+1,组成方程组:$\left\{\begin{array}{l}\frac{{x}^{2}}{2}+{y}^{2}=1\\ y=x+1\end{array}\right.$,消去y可得:3x2+4x=0,
设A(x1,y1) B(x2,y2),解得x1=0,x2=-$\frac{4}{3}$,
AB=$\sqrt{1+{k}^{2}}$|x1-x2|=$\frac{4\sqrt{2}}{3}$.
F2(1,0)到直线AB的距离为:d=$\frac{2}{\sqrt{2}}$=$\sqrt{2}$
${S}_{{△ABF}_{2}}$=$\frac{1}{2}$|AB|d=$\frac{1}{2}×\frac{4\sqrt{2}}{3}×\sqrt{2}$=$\frac{4}{3}$.
△ABF2的面积:$\frac{4}{3}$.
点评 本题考查的知识要点:点斜式直线方程,弦长公式的应用,点到直线的距离及相关的运算问题.

练习册系列答案
相关题目
18.某研究机构对高二学生的记忆力x和判断力y进行统计分析,得下表数据
(1)请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$;
(2)试根据(1)求出的线性回归方程,预测记忆力为9的同学的判断力.
($\widehat{b}=\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$,$\widehat{a}=\overline{y}-\widehat{b}\overline{x}$)
| x | 6 | 8 | 10 | 12 |
| y | 3 | 4 | 6 | 7 |
(2)试根据(1)求出的线性回归方程,预测记忆力为9的同学的判断力.
($\widehat{b}=\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$,$\widehat{a}=\overline{y}-\widehat{b}\overline{x}$)
2.已知几何体的三视图(如图),则该几何体的表面积为( )
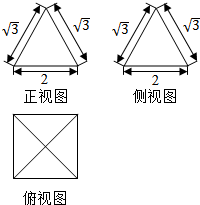

| A. | $4\sqrt{2}$ | B. | $4\sqrt{3}$ | C. | 4$\sqrt{2}$+4 | D. | 4$\sqrt{3}$+4 |
19.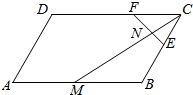 如图平行四边形ABCD中,$\overrightarrow{AB}$=$\overrightarrow{b}$,$\overrightarrow{AD}$=$\overrightarrow{d}$,F是CD的三等分点,E是BC中点,M是AB中点,MC∩EF=N,若$\overrightarrow{MN}$=λ1$\overrightarrow{b}$+λ2$\overrightarrow{d}$,则λ1+λ2=( )
如图平行四边形ABCD中,$\overrightarrow{AB}$=$\overrightarrow{b}$,$\overrightarrow{AD}$=$\overrightarrow{d}$,F是CD的三等分点,E是BC中点,M是AB中点,MC∩EF=N,若$\overrightarrow{MN}$=λ1$\overrightarrow{b}$+λ2$\overrightarrow{d}$,则λ1+λ2=( )
 如图平行四边形ABCD中,$\overrightarrow{AB}$=$\overrightarrow{b}$,$\overrightarrow{AD}$=$\overrightarrow{d}$,F是CD的三等分点,E是BC中点,M是AB中点,MC∩EF=N,若$\overrightarrow{MN}$=λ1$\overrightarrow{b}$+λ2$\overrightarrow{d}$,则λ1+λ2=( )
如图平行四边形ABCD中,$\overrightarrow{AB}$=$\overrightarrow{b}$,$\overrightarrow{AD}$=$\overrightarrow{d}$,F是CD的三等分点,E是BC中点,M是AB中点,MC∩EF=N,若$\overrightarrow{MN}$=λ1$\overrightarrow{b}$+λ2$\overrightarrow{d}$,则λ1+λ2=( )| A. | $\frac{15}{14}$ | B. | 1 | C. | $\frac{5}{14}$ | D. | -$\frac{5}{14}$ |
20.函数y=2sin(3x+$\frac{π}{6}$),x∈R的最小正周期是( )
| A. | $\frac{π}{3}$ | B. | $\frac{2π}{3}$ | C. | $\frac{3π}{2}$ | D. | π |
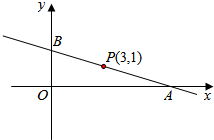 过点P(3,1)作直线l.
过点P(3,1)作直线l.