题目内容
定点A(-1,-
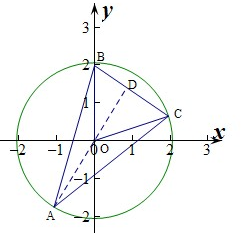
)在定圆x2+y2=4上,且A对于动弦BC的张角为30°,求△ABC面积最大值与此时B,C的坐标.
| 3 |
考点:直线与圆相交的性质
专题:计算题,解三角形
分析:根据正弦定理,结合三角形的面积公式进行化简,求出三角形面积最大的条件,然后根据角之间的关系,求出直线OB,OC的倾斜角,即可得到结论.
解答:
解:x2+y2=4,R=2,∠BAC=30°,B+C=150°
AB=2RsinC=4sinC,AC=4sinB
三角形ABC的面积
=
AB•AC•sin∠BAC
=
×4sinC•4sinB•sin30°
=4sinC•sinB
=-2[cos(B+C)-cos(B-C)]
=-2[cos150°-cos(B-C)]
=-2[-
-cos(B-C)]
=
+2cos(B-C)
∴当∠B=∠C时,cos(B-C)=2,
∵∠BAC=30°,
∴∠B=∠C=75°,
此时三角形ABC的面积的最大值为2+
.
此时BC=2RsinA=4×
=2,
则∵A(-1,-
),
∴直线AO的效率k=
,即∠DOx=60°,
∵OB=OC=BC=2,
∴∠BOC=60°,∴∠DOC=30°
即∠COx=60°-30°=30°,
∴直线OC的倾斜角为30°,直线OB的倾斜角为60°+30°=90°,
∴C点的坐标为(2cos30°,2sin30°),即(
,1),
B点的坐标为(0,2).
AB=2RsinC=4sinC,AC=4sinB
三角形ABC的面积
=
| 1 |
| 2 |
=
| 1 |
| 2 |
=4sinC•sinB
=-2[cos(B+C)-cos(B-C)]
=-2[cos150°-cos(B-C)]
=-2[-
| ||
| 2 |
=
| 3 |
∴当∠B=∠C时,cos(B-C)=2,
∵∠BAC=30°,
∴∠B=∠C=75°,
此时三角形ABC的面积的最大值为2+
| 3 |

此时BC=2RsinA=4×
| 1 |
| 2 |
则∵A(-1,-
| 3 |
∴直线AO的效率k=
| 3 |
∵OB=OC=BC=2,
∴∠BOC=60°,∴∠DOC=30°
即∠COx=60°-30°=30°,
∴直线OC的倾斜角为30°,直线OB的倾斜角为60°+30°=90°,
∴C点的坐标为(2cos30°,2sin30°),即(
| 3 |
B点的坐标为(0,2).
点评:本题主要考查正弦定理的应用,考查学生的计算能力.根据条件求出直线OB,OC的倾斜角是解决本题的关键.

练习册系列答案
 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案 小题狂做系列答案
小题狂做系列答案
相关题目
各项均为正数的等比数列{an}中,2a1+a2=a3,则
的值为( )
| a4+a5 |
| a3+a4 |
| A、-1 | B、-1或2 | C、3 | D、2 |

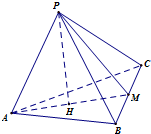 (理科)如图,正三棱锥P-ABC中,底面ABC的边长为2,正三棱锥P-ABC的体积为V=1,M为线段BC的中点,求直线PM与平面ABC所成的角(结果用反三角函数值表示).
(理科)如图,正三棱锥P-ABC中,底面ABC的边长为2,正三棱锥P-ABC的体积为V=1,M为线段BC的中点,求直线PM与平面ABC所成的角(结果用反三角函数值表示).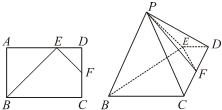 如图,在矩形ABCD中,点E为边AD上的点,点F为边CD的中点,AB=AE=
如图,在矩形ABCD中,点E为边AD上的点,点F为边CD的中点,AB=AE=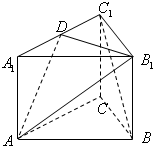 如图,三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,底面△ABC是边长为a的正三角形,侧棱长为
如图,三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,底面△ABC是边长为a的正三角形,侧棱长为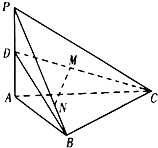 如图,在四面体P-ABC中,PA⊥平面ABC,AB⊥BC,PA=2,AC=2
如图,在四面体P-ABC中,PA⊥平面ABC,AB⊥BC,PA=2,AC=2