题目内容
各项均为正数的等比数列{an}中，2a1+a2=a3，则
的值为（ ）
| a4+a5 |
| a3+a4 |
| A、-1 | B、-1或2 | C、3 | D、2 |
考点：等比数列的性质
专题：等差数列与等比数列
分析：根据等比数列的通项公式求出公比，即可得到结论．
解答：
解：∵2a1+a2=a3，
∴2a1+a1q=a1q2，
即q2-q-2=0，
解当q=2或q=-1，
∵各项均为正数的等比数列{an}，
∴q＞0，
即q=2，
则
=q=2，
故选：D．
∴2a1+a1q=a1q2，
即q2-q-2=0，
解当q=2或q=-1，
∵各项均为正数的等比数列{an}，
∴q＞0，
即q=2，
则
| a4+a5 |
| a3+a4 |
故选：D．
点评：本题主要考查等比数列的运算性质，根据条件求出公比是解决本题的关键，比较基础．
练习册系列答案
100分闯关期末冲刺系列答案
相关题目
关于直线a，b及平面α，β，下列命题中正确的是（ ）
| A、若a∥α，α∩β=b，则a∥b |
| B、若a∥α，b∥α，则a∥b |
| C、若a⊥α，a∥β，则α⊥β |
| D、若a∥α，b⊥a，则b⊥α |
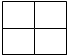由单位正方体（棱长为1的正方体）叠成的积木堆的正视图与侧视图均为图所示，则该积木堆中单位正方体的最少个数为（ ）| A、5个 | B、4个 | C、6个 | D、7个 |
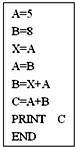
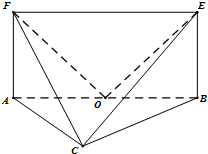如图，平面ABEF⊥平面ABC，四边形ABEF为矩形，△ABC为等边三角形． O为AB的中点，OF⊥EC．
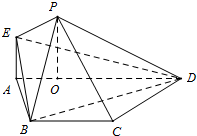如图，在等腰梯形ABCD中，AD∥BC，AB=BC=CD=