题目内容
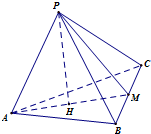 (理科)如图,正三棱锥P-ABC中,底面ABC的边长为2,正三棱锥P-ABC的体积为V=1,M为线段BC的中点,求直线PM与平面ABC所成的角(结果用反三角函数值表示).
(理科)如图,正三棱锥P-ABC中,底面ABC的边长为2,正三棱锥P-ABC的体积为V=1,M为线段BC的中点,求直线PM与平面ABC所成的角(结果用反三角函数值表示).考点:直线与平面所成的角
专题:综合题,空间角
分析:连接AM,过点P作PH垂直于AM于H,证明∠PMH为直线PM与平面ABC所成的角(或其补角),利用正三棱锥P-ABC底面ABC的边长为2,体积为V=1,可得PH,求出HM,即可得出结论.
解答:
 解:如图,连接AM,过点P作PH垂直于AM于H,
解:如图,连接AM,过点P作PH垂直于AM于H,
正三棱锥P-ABC中,
⇒BC⊥平面PMA 3分
又PH为平面PMA中的一条直线,
所以BC⊥PH
因为PH⊥AM且BC∩AM=M,
所以PH⊥平面ABC,5分
所以∠PMH为直线PM与平面ABC所成的角(或其补角) 6分
因为正三棱锥P-ABC底面ABC的边长为2,体积为V=1
所以由V=
S△ABCPH知PH=
=
=
,
⇒H为△ABC的重心,
所以HM=
AM=
,9分
Rt△PHM中,tan∠PMH=
=
=3 11分
得∠PMH=arctan3,
故直线PM与平面ABC所成的角为arctan3(或arccos
或arcsin
) 12分
 解:如图,连接AM,过点P作PH垂直于AM于H,
解:如图,连接AM,过点P作PH垂直于AM于H,正三棱锥P-ABC中,
|
又PH为平面PMA中的一条直线,
所以BC⊥PH
因为PH⊥AM且BC∩AM=M,
所以PH⊥平面ABC,5分
所以∠PMH为直线PM与平面ABC所成的角(或其补角) 6分
因为正三棱锥P-ABC底面ABC的边长为2,体积为V=1
所以由V=
| 1 |
| 3 |
| 3V |
| S△ABC |
| 3 | ||||
|
| 3 |
|
所以HM=
| 1 |
| 3 |
| ||
| 3 |
Rt△PHM中,tan∠PMH=
| PH |
| HM |
| ||||
|
得∠PMH=arctan3,
故直线PM与平面ABC所成的角为arctan3(或arccos
| ||
| 10 |
3
| ||
| 10 |
点评:本题考查线面角,考查线面垂直的证明,考查学生分析解决问题的能力,正确作出线面角是关键.

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目
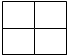 由单位正方体(棱长为1的正方体)叠成的积木堆的正视图与侧视图均为图所示,则该积木堆中单位正方体的最少个数为( )
由单位正方体(棱长为1的正方体)叠成的积木堆的正视图与侧视图均为图所示,则该积木堆中单位正方体的最少个数为( )| A、5个 | B、4个 | C、6个 | D、7个 |
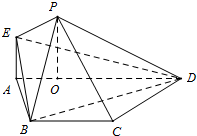 如图,在等腰梯形ABCD中,AD∥BC,AB=BC=CD=
如图,在等腰梯形ABCD中,AD∥BC,AB=BC=CD=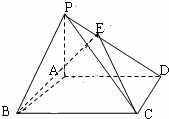 (理科)已知如图,四边形ABCD是矩形,PA⊥面ABCD,其中AB=3,PA=4.若在PD上存在一点E,使得BE⊥CE.
(理科)已知如图,四边形ABCD是矩形,PA⊥面ABCD,其中AB=3,PA=4.若在PD上存在一点E,使得BE⊥CE.