题目内容
PA，PC分别切⊙O于A，C，AB是⊙O的直径，CD⊥AB于D，PB交CD于E，求证：ED=EC．
考点：与圆有关的比例线段,弦切角
专题：直线与圆
分析：过点B作BF⊥AB交PC的延长线于点F．利用圆的切线性质可得PA∥CD∥BF．再根据比例线段的性质即可证明结论．
解答：
证明：如图，过点B作BF⊥AB交PC的延长线于点F．
∵PA，PF，BF都与⊙O相切，
∴PA=PC，BF=CF．
又∵PA⊥AB，BF⊥AB，CD⊥AB，
∴PA∥CD∥BF．
∴
=
=
=
=
=
．
∴ED=EC．
证明：如图，过点B作BF⊥AB交PC的延长线于点F．∵PA，PF，BF都与⊙O相切，
∴PA=PC，BF=CF．
又∵PA⊥AB，BF⊥AB，CD⊥AB，
∴PA∥CD∥BF．
∴
| ED |
| PA |
| BD |
| BA |
| CF |
| PF |
| BF |
| PF |
| EC |
| PC |
| EC |
| PA |
∴ED=EC．
点评：本题考查圆的切线性质，平行线分线段成比例定理等知识．属于中档题．
练习册系列答案
阅读快车系列答案
相关题目
关于直线a，b及平面α，β，下列命题中正确的是（ ）
| A、若a∥α，α∩β=b，则a∥b |
| B、若a∥α，b∥α，则a∥b |
| C、若a⊥α，a∥β，则α⊥β |
| D、若a∥α，b⊥a，则b⊥α |
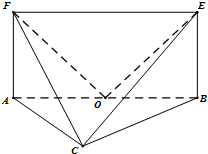如图，平面ABEF⊥平面ABC，四边形ABEF为矩形，△ABC为等边三角形． O为AB的中点，OF⊥EC．
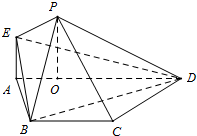如图，在等腰梯形ABCD中，AD∥BC，AB=BC=CD=
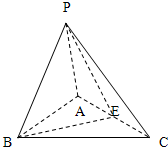如图，在三棱锥P-ABC中，PA=PB=AB=2，AB⊥BC，平面PAB⊥平面ABC，E为AC的中点．
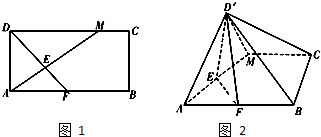如图1，在矩形ABCD中，AB=2BC，点M在边CD上，点F在边AB上，且DF⊥AM，垂足为E，若将△ADM沿AM折起，使点D位于D′位置，连接D′B，D′C得如图2四棱锥D′-ABCM．