题目内容
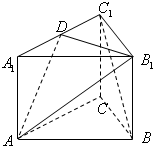 如图,三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,底面△ABC是边长为a的正三角形,侧棱长为
如图,三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,底面△ABC是边长为a的正三角形,侧棱长为
| ||
| 2 |
(1)若A1D=DC1,求证:直线BC1∥平面AB1D;
(2)求AB1与侧面BCC1B1所成角的大小;
(3)请在棱A1C1确定点D的位置,使二面角A1-AB1-D的平面角为
| π |
| 4 |
考点:与二面角有关的立体几何综合题
专题:空间位置关系与距离,空间角
分析:(1)连接A1B交AB1于E点,由A1D=DC1,结合三角形中位线定理可得DE∥BC1,进而根据线面平行的判定定理得到直线BC1∥平面AB1D;
(2)取BC中点F,连DF,B1F,∠DB1F为DB1与平面BCC1B1所成角.在直角△DB1F中求解即可.
(3)连接MN,过A1作A1F⊥AB1于F.由(2)的结合可得∠MND为二面角A1-AB1-D平面角,设,由二面角A1-AB1-D平面角的正切值的大小为1,我们易构造关于λ的方程,解方程求出λ的值,即可指出点D的位置.
(2)取BC中点F,连DF,B1F,∠DB1F为DB1与平面BCC1B1所成角.在直角△DB1F中求解即可.
(3)连接MN,过A1作A1F⊥AB1于F.由(2)的结合可得∠MND为二面角A1-AB1-D平面角,设,由二面角A1-AB1-D平面角的正切值的大小为1,我们易构造关于λ的方程,解方程求出λ的值,即可指出点D的位置.
解答:
 解:(1)证明:连接A1B交AB1于E点,
解:(1)证明:连接A1B交AB1于E点,
在平行四边形ABB1A1中,有A1E=BE,又A1D=DC1
∴DE为△A1BC1的中位线,从而DE∥BC1,
又DE?平面AB1D,BC1?平面AB1D,
∴直线BC1∥平面AB1D
(2)取BC中点F,连AF,B1F
∵三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,底面△ABC是边长为a的正三角形,
又AC=a,BC=a,AB=a知AF⊥BC,∴AF⊥面BCC1B1
又F为BC中点,∴DF=
a,⊥面BCC1B1
∴AB1在平面BCC1B1内的射影为FB1
∴AB1与平面BCC1B1的所成角为∠AB1F
在RT△FB1A中,B1B=
a,BF=
=
a,
∴∠AB1F=45°.
(3)连接MN,过A1作A1F⊥AB1于F.
由(2)中的作法可知:∠MND为二面角A1-AB1-D平面角,
设
=λ,则
=
,
则可得DM=
λ,A1F=
a,
=1-
⇒MN=
(1-
),
∴tanθ=
=
=-3+
.∴-3+
=1⇒λ=
即点D在棱A1C1上,且
=
时,
二面角A1-AB1-D平面角的正切值的大小为
.
 解:(1)证明:连接A1B交AB1于E点,
解:(1)证明:连接A1B交AB1于E点,在平行四边形ABB1A1中,有A1E=BE,又A1D=DC1
∴DE为△A1BC1的中位线,从而DE∥BC1,
又DE?平面AB1D,BC1?平面AB1D,
∴直线BC1∥平面AB1D
(2)取BC中点F,连AF,B1F
∵三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,底面△ABC是边长为a的正三角形,
又AC=a,BC=a,AB=a知AF⊥BC,∴AF⊥面BCC1B1
又F为BC中点,∴DF=
| ||
| 2 |
∴AB1在平面BCC1B1内的射影为FB1
∴AB1与平面BCC1B1的所成角为∠AB1F
在RT△FB1A中,B1B=
| ||
| 2 |
(
|
| ||
| 2 |
∴∠AB1F=45°.
(3)连接MN,过A1作A1F⊥AB1于F.
由(2)中的作法可知:∠MND为二面角A1-AB1-D平面角,

设
| A1D |
| A1C1 |
| A1M |
| A1B1 |
| λ |
| 2 |
则可得DM=
| ||
| 2 |
| ||
| 3 |
| MN |
| A1F |
| λ |
| 2 |
| ||
| 3 |
| λ |
| 2 |
∴tanθ=
| DM |
| MN |
| ||||||
|
| 6 |
| 2-λ |
| 6 |
| 2-λ |
| 1 |
| 2 |
即点D在棱A1C1上,且
| A1D |
| A1C1 |
| 1 |
| 2 |
二面角A1-AB1-D平面角的正切值的大小为
| π |
| 4 |
点评:本题考查的知识点是与二面角有关的立体几何综合体,直线与平面平行的判定,平面与平面垂直的判定,其中(1)的关键是证得DE∥BC1,(2)解题的关键是找出直线与平面所成角;(3)解题的关键是根据已知条件构造关于λ的方程.

练习册系列答案
相关题目
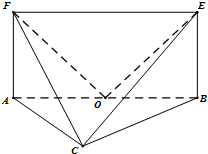 如图,平面ABEF⊥平面ABC,四边形ABEF为矩形,△ABC为等边三角形. O为AB的中点,OF⊥EC.
如图,平面ABEF⊥平面ABC,四边形ABEF为矩形,△ABC为等边三角形. O为AB的中点,OF⊥EC.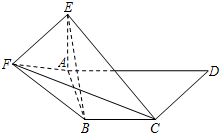 如图,在直角梯形ABCD中,AD∥BC,∠ADC=90°,AE⊥平面ABCD,EF∥CD,BC=CD=AE=EF=
如图,在直角梯形ABCD中,AD∥BC,∠ADC=90°,AE⊥平面ABCD,EF∥CD,BC=CD=AE=EF= 如图,AB是圆O的直径,点C是圆O上不同于A、B的一点,∠BAC=45°,点V是圆O所在平面外一点,且VA=VB=VC,E是AC的中点.
如图,AB是圆O的直径,点C是圆O上不同于A、B的一点,∠BAC=45°,点V是圆O所在平面外一点,且VA=VB=VC,E是AC的中点.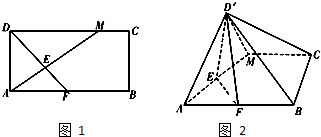 如图1,在矩形ABCD中,AB=2BC,点M在边CD上,点F在边AB上,且DF⊥AM,垂足为E,若将△ADM沿AM折起,使点D位于D′位置,连接D′B,D′C得如图2四棱锥D′-ABCM.
如图1,在矩形ABCD中,AB=2BC,点M在边CD上,点F在边AB上,且DF⊥AM,垂足为E,若将△ADM沿AM折起,使点D位于D′位置,连接D′B,D′C得如图2四棱锥D′-ABCM.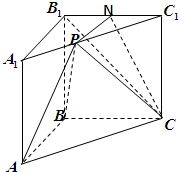 如图,在三棱柱ABC-A1B1C1中,AA1⊥平面ABC,AB⊥BC,且AB=BC=2,点N为B1C1的中点,点P在棱A1C1的运动
如图,在三棱柱ABC-A1B1C1中,AA1⊥平面ABC,AB⊥BC,且AB=BC=2,点N为B1C1的中点,点P在棱A1C1的运动