题目内容
如果函数f(x)=ax(ax-3a2-1)(a>0且a≠0)在区间[0,+∞)单调递增,那么实数a的取值范围是什么?
考点:指数函数综合题
专题:函数的性质及应用
分析:利用换元法将函数转化为一元二次函数形式,利用符合函数单调性之间的关系即可得到结论.
解答:
解:设t=ax,当x≥0时,
则函数f(x)=ax(ax-3a2-1)(a>0且a≠0)等价为:
y=g(t)=t(t-3a2-1)=t2-(3a2+1)t,
对称轴t=
若a>1,则当x≥0时,t≥1,此时函数t=ax单调递增,
要使函数f(x)在区间[0,+∞)单调递增,
则g(t)在[1,+∞)单调递增,
即对称轴t=
≤1,即3a2≤1,
即0<a<
,此时不成立,
若0<a<1,则当x≥0时,则0<t≤1,此时函数t=ax单调递减,
要使函数f(x)在区间[0,+∞)单调递增,
则g(t)在0<t≤1单调递减,
即对称轴t=
≥1,即3a2≥1,
即
≤a<1,
即实数a的取值范围是
≤a<1.
则函数f(x)=ax(ax-3a2-1)(a>0且a≠0)等价为:
y=g(t)=t(t-3a2-1)=t2-(3a2+1)t,
对称轴t=
| 3a2+1 |
| 2 |
若a>1,则当x≥0时,t≥1,此时函数t=ax单调递增,
要使函数f(x)在区间[0,+∞)单调递增,
则g(t)在[1,+∞)单调递增,
即对称轴t=
| 3a2+1 |
| 2 |
即0<a<
| ||
| 3 |
若0<a<1,则当x≥0时,则0<t≤1,此时函数t=ax单调递减,
要使函数f(x)在区间[0,+∞)单调递增,
则g(t)在0<t≤1单调递减,
即对称轴t=
| 3a2+1 |
| 2 |
即
| ||
| 3 |
即实数a的取值范围是
| ||
| 3 |
点评:本题主要考查符合函数单调性的应用,根据同增异减的原则是解决本题的根据,本题还使用了换元法,注意对a要进行分类讨论.

练习册系列答案
 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目
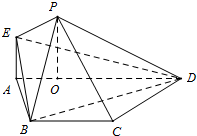 如图,在等腰梯形ABCD中,AD∥BC,AB=BC=CD=
如图,在等腰梯形ABCD中,AD∥BC,AB=BC=CD= 如图,AB是圆O的直径,点C是圆O上不同于A、B的一点,∠BAC=45°,点V是圆O所在平面外一点,且VA=VB=VC,E是AC的中点.
如图,AB是圆O的直径,点C是圆O上不同于A、B的一点,∠BAC=45°,点V是圆O所在平面外一点,且VA=VB=VC,E是AC的中点.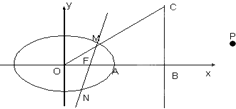 已知椭圆
已知椭圆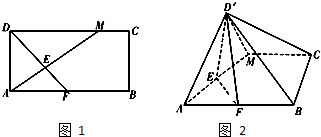 如图1,在矩形ABCD中,AB=2BC,点M在边CD上,点F在边AB上,且DF⊥AM,垂足为E,若将△ADM沿AM折起,使点D位于D′位置,连接D′B,D′C得如图2四棱锥D′-ABCM.
如图1,在矩形ABCD中,AB=2BC,点M在边CD上,点F在边AB上,且DF⊥AM,垂足为E,若将△ADM沿AM折起,使点D位于D′位置,连接D′B,D′C得如图2四棱锥D′-ABCM.