题目内容
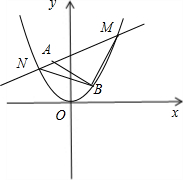
已知抛物线 x2=y,直线L经过点A(-1,2)但不经过点B(1,1),与抛物线交于M,N两点,点M的横坐标大于1,直线L的斜率为k,直线BN,BM的斜率分别为k1,k2.
(1)当AB垂直于直线L时,求 k1.k2的值.
(2)设△BAM和△BAN的面积分别为S1,S2,当k≤1时,求
的取值范围.
(1)当AB垂直于直线L时,求 k1.k2的值.
(2)设△BAM和△BAN的面积分别为S1,S2,当k≤1时,求
| S1 |
| S2 |
考点:直线与圆锥曲线的关系,直线的一般式方程与直线的垂直关系
专题:圆锥曲线中的最值与范围问题
分析:(1)利用相互垂直的直线斜率之间的关系可得直线L的斜率及其方程,进而与抛物线的方程联立可得交点M,N的坐标,再利用斜率计算公式即可得出;
(2)把直线L的方程与抛物线的方程联立可得交点M,N的坐标,再利用两点间的距离公式可得
=
=
,由k的取值范围即可得出.
(2)把直线L的方程与抛物线的方程联立可得交点M,N的坐标,再利用两点间的距离公式可得
| S1 |
| S2 |
| |AM| |
| |AN| |
| ||
|
解答:
解:(1)kAB=
=-
,
∵AB⊥L,
∴kAB•kL=-1,∴kL=2.
∴直线L的方程为:y-2=2(x+1),化为2x-y+4=0.
联立
,解得
,
.
∴M(1+
,6+2
),N(1-
,6-2
).
∴k1=
=2-
,k2=
=2+
.
(2)设M(x1,y1),N(x2,y2).
直线L的方程为y-2=k(x+1),化为y=kx+k+2.
联立
,化为x2-kx-k-2=0,
x1+x2=k,x1x2=-k-2.
x=
,
∵x1>1,
∴x1=
,x2=
.
由x1=
>1,化为
>2-k,又k≤1,
解得1≥k>-
.
∴
=
=
=
=
=
=
=f(k),
∵-
<k≤1,∴f(k)单调递增.
∴f(-
)<f(k)≤f(1),
即4<f(k)≤
.
| 2-1 |
| -1-1 |
| 1 |
| 2 |

∵AB⊥L,
∴kAB•kL=-1,∴kL=2.
∴直线L的方程为:y-2=2(x+1),化为2x-y+4=0.
联立
|
|
|
∴M(1+
| 5 |
| 5 |
| 5 |
| 5 |
∴k1=
6-2
| ||
1-
|
| 5 |
6+2
| ||
1+
|
| 5 |
(2)设M(x1,y1),N(x2,y2).
直线L的方程为y-2=k(x+1),化为y=kx+k+2.
联立
|
x1+x2=k,x1x2=-k-2.
x=
k±
| ||
| 2 |
∵x1>1,
∴x1=
k+
| ||
| 2 |
k-
| ||
| 2 |
由x1=
k+
| ||
| 2 |
| k2+4k+8 |
解得1≥k>-
| 1 |
| 2 |
∴
| S1 |
| S2 |
| |AM| |
| |AN| |
| ||
|
=
| ||
|
=
| |x1+1| |
| |x2+1| |
=
| ||
|
k2+4k+6+(k+2)
| ||
| 2 |
∵-
| 1 |
| 2 |
∴f(-
| 1 |
| 2 |
即4<f(k)≤
11+3
| ||
| 2 |
点评:本题考查了相互垂直的直线斜率之间的关系、直线与抛物线相交转化为的方程联立可得交点的坐标、斜率计算公式、两点间的距离公式、函数的单调性,属于难题.

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案 全优冲刺100分系列答案
全优冲刺100分系列答案
相关题目
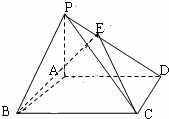 (理科)已知如图,四边形ABCD是矩形,PA⊥面ABCD,其中AB=3,PA=4.若在PD上存在一点E,使得BE⊥CE.
(理科)已知如图,四边形ABCD是矩形,PA⊥面ABCD,其中AB=3,PA=4.若在PD上存在一点E,使得BE⊥CE.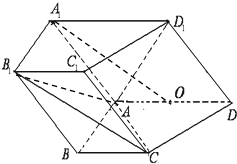 如图,在四棱柱ABCD-A1B1C1D1中,侧面ADD1A1⊥底面ABCD,D1A=D1D=
如图,在四棱柱ABCD-A1B1C1D1中,侧面ADD1A1⊥底面ABCD,D1A=D1D=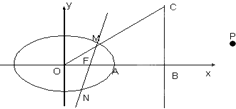 已知椭圆
已知椭圆 如图,多面体ABCDEF中,BA,BC,BE两两垂直,且AB∥EF,CD∥BE,AB=BE=2,BC=CD=EF=1.
如图,多面体ABCDEF中,BA,BC,BE两两垂直,且AB∥EF,CD∥BE,AB=BE=2,BC=CD=EF=1.