题目内容
已知{an}是等比数列,其中a1,a8是关于x的方程x2-2xsinα-
sinα=0的两根,且(a1+a8)2=2a3a6+6,则锐角α的值为( )
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:等比数列的性质,函数的零点,等比数列的通项公式
专题:计算题,等差数列与等比数列,三角函数的求值
分析:由已知条件运用韦达定理推导出a1+a8=2sinα,a1•a8=a3a6=-
sinα,由(a1+a8)2=2a3a6+6,得4sin2α=6-2
sinα,由此能求出锐角α的值.
| 3 |
| 3 |
解答:
解:∵{an}是等比数列,a1和a8是关于x的方程x2-2xsinα-
sinα=0的两根,
∴a1+a8=2sinα,a1•a8=a3a6=-
sinα,
∵(a1+a8)2=2a3a6+6,
∴4sin2α=6-2
sinα,解得sinα=
,
∴锐角α的值为
.
故选C.
| 3 |
∴a1+a8=2sinα,a1•a8=a3a6=-
| 3 |
∵(a1+a8)2=2a3a6+6,
∴4sin2α=6-2
| 3 |
| ||
| 2 |
∴锐角α的值为
| π |
| 3 |
故选C.
点评:本题考查等比数列的性质和运用,考查三角函数的求值,注意特殊角的三角函数值,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
函数y=2sin(2x+
)是( )
| π |
| 2 |
| A、周期为π的偶函数 |
| B、周期为π的奇函数 |
| C、周期为2π的偶函数 |
| D、周期为2π的奇函数 |
已知7sinα-24cosα=25,则tanα=( )
A、±
| ||
B、±
| ||
C、-
| ||
D、-
|
设数列{an}是公差d<0的等差数列,Sn为其前n项和,若S6=5a1+10d,则Sn取最大值时,n=( )
| A、5 | B、6 | C、5或6 | D、6或7 |
已知某个几何体的三视图如右图,根据图中标出的尺寸可得这个几何体的体积是( )
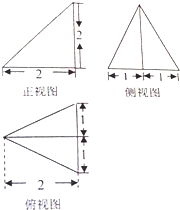

A、
| ||
B、
| ||
C、
| ||
D、
|