题目内容
设数列{an}是公差d＜0的等差数列，Sn为其前n项和，若S6=5a1+10d，则Sn取最大值时，n=（ ）
| A、5 | B、6 | C、5或6 | D、6或7 |
考点：等差数列的性质
专题：计算题,等差数列与等比数列
分析：利用S6=5a1+10d，可得a6=0，根据数列{an}是公差d＜0的等差数列，即可得出结论．
解答：
解：∵S6=5a1+10d，
∴6a1+15d=5a1+10d得到a1+5d=0即a6=0，
∵数列{an}是公差d＜0的等差数列，
∴n=5或6，Sn取最大值．
故选：C．
∴6a1+15d=5a1+10d得到a1+5d=0即a6=0，
∵数列{an}是公差d＜0的等差数列，
∴n=5或6，Sn取最大值．
故选：C．
点评：本题考查等差数列的性质，考查等差数列的通项与求和，比较基础．
练习册系列答案
相关题目
下列判断正确的是（ ）
| A、二次函数一定有零点 |
| B、奇函数一定有零点 |
| C、偶函数一定有零点 |
| D、以上说法均不正确 |
已知{an}是等比数列，其中a1，a8是关于x的方程x2-2xsinα-
sinα=0的两根，且（a1+a8）2=2a3a6+6，则锐角α的值为（ ）
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|
已知f（x）=
，则f（-1）+f（4）的值是（ ）
|
| A、-7 | B、3 | C、-8 | D、4 |
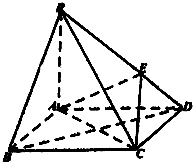如图，在底面是菱形的四棱锥P-ABCD中，∠ABC=60°，PA=AC=a，PB=PD=