题目内容
2.在平行六面体ABCD-A${\;}_{{1}_{\;}}$B1C1D1中,$\overrightarrow{A{C}_{1}}$=x$\overrightarrow{AB}$+2y$\overrightarrow{BC}$+3z$\overrightarrow{{C}_{1}C}$,则x+y+z=( )| A. | 1 | B. | $\frac{7}{6}$ | C. | $\frac{5}{6}$ | D. | $\frac{2}{3}$ |
分析 如图所示,在平行六面体ABCD-A${\;}_{{1}_{\;}}$B1C1D1中,$\overrightarrow{A{C}_{1}}$=$\overrightarrow{AB}$+$\overrightarrow{BC}$+$\overrightarrow{C{C}_{1}}$=$\overrightarrow{AB}$+$\overrightarrow{BC}$-$\overrightarrow{{C}_{1}C}$,与$\overrightarrow{A{C}_{1}}$=x$\overrightarrow{AB}$+2y$\overrightarrow{BC}$+3z$\overrightarrow{{C}_{1}C}$比较即可得出.
解答 解:如图所示,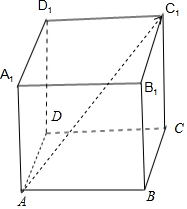
在平行六面体ABCD-A${\;}_{{1}_{\;}}$B1C1D1中,
$\overrightarrow{A{C}_{1}}$=$\overrightarrow{AB}$+$\overrightarrow{BC}$+$\overrightarrow{C{C}_{1}}$=$\overrightarrow{AB}$+$\overrightarrow{BC}$-$\overrightarrow{{C}_{1}C}$,
与$\overrightarrow{A{C}_{1}}$=x$\overrightarrow{AB}$+2y$\overrightarrow{BC}$+3z$\overrightarrow{{C}_{1}C}$比较可得:
x=1,2y=1,-1=3z.
则x+y+z=1+$\frac{1}{2}$-$\frac{1}{3}$=$\frac{7}{6}$.
故选:B.
点评 本题考查了空间平行六面体法则、空间向量基本定理、数形结合方法,考查了推理能力与计算能力,属于基础题.

| 日车流量x | 0≤x<5 | 5≤x<10 | 10≤x<15 | 15≤x<20 | 20≤x<25 | x≥25 |
| 频率 | 0.05 | 0.25 | 0.35 | 0.25 | 0.10 | 0 |
(Ⅰ)求在未来连续3天里,有连续2天的日车流量都不低于10万辆且另1天的日车流量低于5万辆的概率;
(Ⅱ)用X表示在未来3天时间里日车流量不低于10万辆的天数,求X的分布列、数学期望以及方差.
| ξ | -1 | 0 | 1 |
| P | a | $\frac{1}{2}$-a | $\frac{1}{2}$ |
| A. | E(ξ)增大,D(ξ)增大 | B. | E(ξ)减小,D(ξ)增大 | C. | E(ξ)增大,D(ξ)减小 | D. | E(ξ)减小,D(ξ)减小 |
(1)${y_1}=\frac{(x+3)(x-5)}{x+3}$,y2=x-5;
(2)${y_1}=\sqrt{x+1}\sqrt{x-1}$,${y_2}=\sqrt{(x+1)(x-1)}$;
(3)f(x)=x,$g(x)=\sqrt{x^2}$;
(4)f(x)=x,$g(x)=\root{3}{x^3}$;
(5)${f_1}(x)={(\sqrt{2x-5})^2}$,f2(x)=2x-5.
| A. | (1)(2) | B. | (2)(3) | C. | (4) | D. | (3)(5) |
| A. | $\frac{π}{4}$ | B. | -$\frac{3π}{4}$ | C. | $\frac{5π}{4}$ | D. | $\frac{π}{4}$或-$\frac{3π}{4}$ |
| ζ | 1 | 2 | 3 | 4 |
| p | $\frac{1}{4}$ | $\frac{1}{3}$ | $\frac{1}{6}$ | $\frac{1}{4}$ |
| A. | $\frac{179}{16}$ | B. | $\frac{143}{16}$ | C. | $\frac{179}{48}$ | D. | $\frac{136}{48}$ |