题目内容
已知函数y=
x3-3x+9,求函数的极小值.
| 1 |
| 3 |
考点:利用导数研究函数的极值
专题:导数的综合应用
分析:f′(x)=x2-3,令f′(x)=0,解得x=±
.列出表格,利用单调性与极值的关系即可得出.
| 3 |
解答:
解:f′(x)=x2-3,
令f′(x)=0,解得x=±
.
列表如下:
由表格可知:当x=
时,函数f(x)取得极小值,f(
)=
×(
)3-3
+9=9-2
.
令f′(x)=0,解得x=±
| 3 |
列表如下:
| x | (-∞,-
| -
| (-
|
| (
| ||||||||||||
| f′(x) | + | 0 | - | 0 | + | ||||||||||||
| f(x) | 单调递增 | 极大值 | 单调递减 | 极小值 | 单调递增 |
| 3 |
| 3 |
| 1 |
| 3 |
| 3 |
| 3 |
| 3 |
点评:本题查克拉利用导数研究函数的单调性极值,属于基础题.

练习册系列答案
相关题目
设曲线y=
在点(-2,f(2))处的切线与直线ax+y+1=0垂直,则实数a=( )
| x-1 |
| x+1 |
A、-
| ||
B、
| ||
| C、-2 | ||
| D、2 |
在△ABC中,已知6
•
=2
•
=3
•
,则∠A=( )
| AC |
| AB |
| AB |
| BC |
| BC |
| CA |
| A、30° | B、45° |
| C、120° | D、135° |
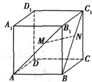 如图,在正方体ABCD-A1B1C1D1中,M、N分别是对角线AB1、BC1上的点,且
如图,在正方体ABCD-A1B1C1D1中,M、N分别是对角线AB1、BC1上的点,且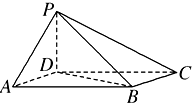 如图,四棱锥P-ABCD中,底面ABCD为平行四边形,∠DAB=60°,AB=2,AD=1,PD⊥底面ABCD.
如图,四棱锥P-ABCD中,底面ABCD为平行四边形,∠DAB=60°,AB=2,AD=1,PD⊥底面ABCD.