题目内容
已知函数f（x）=
，若f（a）+f（1）=0，则实数a的值等于（ ）
|
| A、3 | B、1 | C、-3 | D、-1 |
考点：函数的值
专题：函数的性质及应用
分析：首先根据分段函数的解析式，对a的范围进行讨论，进一步根据不同的范围求出参数a的结果．
解答：
解：已知函数f（x）=
则：①当a＞0时，f（a）+f（1）=0
得到：2a+2=0
解得：a=-1
与前提条件矛盾故舍去．
②当a＜0时，f（a）+f（1）=0
得到：a+1+2=0
解得：a=-3
综上所述：a=-1
故选：C
|
则：①当a＞0时，f（a）+f（1）=0
得到：2a+2=0
解得：a=-1
与前提条件矛盾故舍去．
②当a＜0时，f（a）+f（1）=0
得到：a+1+2=0
解得：a=-3
综上所述：a=-1
故选：C
点评：本题考查的知识要点：分段函数的应用，分类讨论问题的应用，属于基础题型．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
设f（x）=
，若f（0）是f（x）的最小值，则a的取值范围是（ ）
|
| A、[-1，2] |
| B、[-1，0] |
| C、[1，2] |
| D、[0，2] |
已知数列{an}满足（n+2）an+1=（n+1）an，且a2=
，则an=（ ）
| 1 |
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|
下列命题为真命题的是（ ）
| A、若ac＞bc，则a＞b | ||||
| B、若a2＞b2，则a＞b | ||||
C、若
| ||||
D、若
|
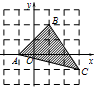已知点A（-1，0），B（1，2），C（3，-1），点P（x，y）为△ABC边界及内部（如图阴影部分）的任意一点，则z=x-2y的最小值为已知直线（a+2）x+y+8=0与直线（2a-1）x-（a+2）y-7=0垂直，则a=（ ）
A、-3±
| ||
| B、0或-2 | ||
| C、1或-2 | ||
D、
|