题目内容
已知数列{an}的前n项和Sn=2an-4(n∈N*).
(1)求a1,a2,a3求数列{an}的通项公式;
(2)若数列{bn}满足:bn+1=an+2bn,且b1=2,求证数列{
}是等差数列;
(3)求数列{bn}的前n项和Sn.
(1)求a1,a2,a3求数列{an}的通项公式;
(2)若数列{bn}满足:bn+1=an+2bn,且b1=2,求证数列{
| bn |
| 2n |
(3)求数列{bn}的前n项和Sn.
考点:数列的求和
专题:等差数列与等比数列
分析:(1)利用条件分别让n=1,2,3即可求a1,a2,a3求数列{an}的通项公式;
(2)根据等差数列的定义即可证明数列{
}是等差数列;
(3)利用错位相减法即可求出数列{bn}的前n项和Sn.
(2)根据等差数列的定义即可证明数列{
| bn |
| 2n |
(3)利用错位相减法即可求出数列{bn}的前n项和Sn.
解答:
解:(1)当n=1时,a1=2a1-4,解得a1=4,
当n=2时,S2=2a2-4=4+a2,解得a2=8,
当n=3时,S3=2a3-4=4+8+a3,解得a3=16,
则数列{an}的通项公式an=2n+1;
(2)若数列{bn}满足:bn+1=an+2bn=2n+1+2bn,且b1=2,
则
=1+
=1+
,
即
-
=1,
故数列{
}是公差d=1的等差数列;
(3)∵数列{
}是公差d=1的等差数列,首项为
=
=1,
∴
=1+n-1=n,即bn=n•2n,
则数列{bn}的前n项和Sn=1•21+2•22+…+(n-1)•2n-1+n•2n,
则2Sn=1•22+2•23+…+(n-1)•2n+n•2n+1,
两式相减得-Sn=1•21+22+…+2n-n•2n+1=
-n•2n+1=2n+1-2-n•2n+1,
∴Sn=(n-1)•2n+1+2.
当n=2时,S2=2a2-4=4+a2,解得a2=8,
当n=3时,S3=2a3-4=4+8+a3,解得a3=16,
则数列{an}的通项公式an=2n+1;
(2)若数列{bn}满足:bn+1=an+2bn=2n+1+2bn,且b1=2,
则
| bn+1 |
| 2n+1 |
| 2bn |
| 2n+1 |
| bn |
| 2n |
即
| bn+1 |
| 2n+1 |
| bn |
| 2n |
故数列{
| bn |
| 2n |
(3)∵数列{
| bn |
| 2n |
| b1 |
| 2 |
| 2 |
| 2 |
∴
| bn |
| 2n |
则数列{bn}的前n项和Sn=1•21+2•22+…+(n-1)•2n-1+n•2n,
则2Sn=1•22+2•23+…+(n-1)•2n+n•2n+1,
两式相减得-Sn=1•21+22+…+2n-n•2n+1=
| 2(1-2n) |
| 1-2 |
∴Sn=(n-1)•2n+1+2.
点评:本题主要考查数列的通项公式的求解以及等差数列的判断,利用错位相减法是解决本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知函数f(x)=
,若f(a)+f(1)=0,则实数a的值等于( )
|
| A、3 | B、1 | C、-3 | D、-1 |
已知集合A={x|-1≤x≤1},B={x|x2-2x≤0},则A∩(∁RB)=( )
| A、[-1,0) |
| B、[-1,0] |
| C、[0,1] |
| D、(-∞,1]∪[2,+∞) |
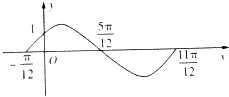 函数f1(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<
函数f1(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<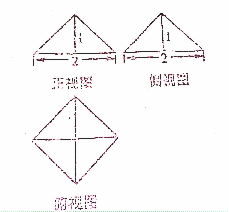 某几何体的三视图如图所示,其中正视图、侧视图均为斜边等于2的等腰直角三角形,俯视图是对角线为2的正方形,则该几何体的内切球的半径等于
某几何体的三视图如图所示,其中正视图、侧视图均为斜边等于2的等腰直角三角形,俯视图是对角线为2的正方形,则该几何体的内切球的半径等于