题目内容
已知直线(a+2)x+y+8=0与直线(2a-1)x-(a+2)y-7=0垂直,则a=( )
A、-3±
| ||
| B、0或-2 | ||
| C、1或-2 | ||
D、
|
考点:直线的一般式方程与直线的垂直关系
专题:直线与圆
分析:对a分类讨论,利用两条直线垂直与斜率的关系即可得出.
解答:
解:a=-2时,两条直线分别化为:y+8=0,-5x-7=0,此时两条直线垂直,a=-2满足条件.
当a≠-2时,两条直线的斜率分别为:-(a+2),
.
∴-(a+2)×
=-1,解得a=1.
综上可得:a=-2或1.
故选:C.
当a≠-2时,两条直线的斜率分别为:-(a+2),
| 2a-1 |
| a+2 |
∴-(a+2)×
| 2a-1 |
| a+2 |
综上可得:a=-2或1.
故选:C.
点评:本题考查了分类讨论、两条直线垂直与斜率的关系,属于基础题.

练习册系列答案
相关题目
已知函数f(x)=
,若f(a)+f(1)=0,则实数a的值等于( )
|
| A、3 | B、1 | C、-3 | D、-1 |
α,β表示不重合的两个平面,m,l表示不重合的两条直线.若α∩β=m,l?α,l?β,则“l∥m”是“l∥α且l∥β”的( )
| A、充分且不必要条件 |
| B、必要且不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
若a∈R,则a=2是(a-1)(a-2)=0的( )
| A、充分而不必要条件 |
| B、必要而不充分条件 |
| C、充要条件 |
| D、既不充分又不必要条件 |
若一个等差数列首项为0,公差为2,则这个等差数列的前20项之和为( )
| A、360 | B、370 |
| C、380 | D、390 |
设i为虚数单位,则复数z=
在复平面内对应的点所在的象限是( )
| 1+i |
| i |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
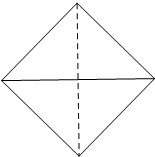 已知四面体S-ABC的所有棱长都相等,它的俯视图是一个边长为
已知四面体S-ABC的所有棱长都相等,它的俯视图是一个边长为