题目内容
已知数列{an}满足(n+2)an+1=(n+1)an,且a2=
,则an=( )
| 1 |
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:数列递推式
专题:计算题,等差数列与等比数列
分析:将(n+2)an+1=(n+1)an化简整理得出
=
,利用累积法求an.
| an+1 |
| an |
| n+1 |
| n+2 |
解答:
解:∵(n+2)an+1=(n+1)an,
∴
=
,
∴
=
,
=
,…
=
以上各式两边分别相乘得an=
(n≥2),
由n=1时也适合上式,所以an=
,
故选:A.
∴
| an+1 |
| an |
| n+1 |
| n+2 |
∴
| a3 |
| a2 |
| 3 |
| 4 |
| a4 |
| a3 |
| 4 |
| 5 |
| an |
| an-1 |
| n |
| n+1 |
以上各式两边分别相乘得an=
| 1 |
| n+1 |
由n=1时也适合上式,所以an=
| 1 |
| n+1 |
故选:A.
点评:本题考查数列通项求解,考查学生的计算能力,利用累积法是关键.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
已知函数f(x)=
,若f(a)+f(1)=0,则实数a的值等于( )
|
| A、3 | B、1 | C、-3 | D、-1 |
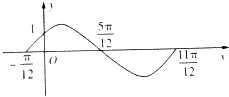 函数f1(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<
函数f1(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<