题目内容
正数a,b满足a+b=1,求ab2的最大值.
考点:基本不等式
专题:不等式的解法及应用
分析:由ab2=4×a×
×
,根据均值不等式求得结果.
| b |
| 2 |
| b |
| 2 |
解答:
解:由a+b=1,且a,b为正数,
∴ab2=4×a×
×
≤4×(
)3=4×(
)3=
,当且仅当a=
,b=
时取等号,
∴ab2的最大值是
.
∴ab2=4×a×
| b |
| 2 |
| b |
| 2 |
a+
| ||||
| 3 |
| 1 |
| 3 |
| 4 |
| 27 |
| 1 |
| 3 |
| 2 |
| 3 |
∴ab2的最大值是
| 4 |
| 27 |
点评:本题主要考查了均值不等式,关键是取等号时的条件,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
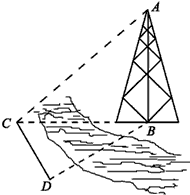 如图所示,测量河对岸的塔高AB时,可以选与塔底B在同一水平面内的两个观测点C与D,测得∠BCD=15°,∠BDC=30°,CD=30m,并在点C处测得塔顶A的仰角为60°,求塔高AB.
如图所示,测量河对岸的塔高AB时,可以选与塔底B在同一水平面内的两个观测点C与D,测得∠BCD=15°,∠BDC=30°,CD=30m,并在点C处测得塔顶A的仰角为60°,求塔高AB.