题目内容
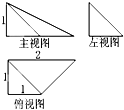
某几何体的三视图如图所示,则该几何体的体积为 .

考点:由三视图求面积、体积
专题:空间位置关系与距离
分析:由已知中的三视图可得:该几何体是一个以俯视图为底面的棱柱,求出底面面积和高,代入棱柱体积公式,可得答案.
解答:
解:由已知中的三视图可得:该几何体是一个以俯视图为底面的棱柱,
其底面面积S=
×(1+2)×1=
,
高h=1,
故棱锥的体积V=
Sh=
×
×1=
,
故答案为:
其底面面积S=
| 1 |
| 2 |
| 3 |
| 2 |
高h=1,
故棱锥的体积V=
| 1 |
| 3 |
| 1 |
| 3 |
| 3 |
| 2 |
| 1 |
| 2 |
故答案为:
| 1 |
| 2 |
点评:本题考查的知识点由三视图求体积和表面积,其中根据已知中的三视图,判断出几何体的形状,是解答的关键.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
已知某个几何体的三视图如图,根据图中标出的尺寸,可得这个几何体的表面积是( )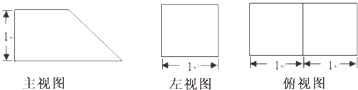

A、
| ||
B、7+
| ||
C、7+2
| ||
D、10+
|
若(
-
)6展开式中的常数项是60,则实数a的值是( )
| x |
| 2 |
| a | ||
|
| A、±1 | ||
B、±
| ||
| C、±2 | ||
D、±2
|
“a≤0”是“函数f(x)=|(ax-1)x|在区间(0,+∞)内单调递增”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
已知△ABC在中,角A,B,C所对的边分别为a,b,c,且acosC+
c=b,则角A( )
| ||
| 2 |
A、
| ||
B、
| ||
C、
| ||
D、
|
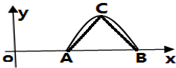 已知函数f(x)=Mcos(ωx+ϕ)(M>0,ω>0,0<ϕ<π)为奇函数,该函数的部分图象如图所示,AC=BC=
已知函数f(x)=Mcos(ωx+ϕ)(M>0,ω>0,0<ϕ<π)为奇函数,该函数的部分图象如图所示,AC=BC=